[t.teschner]

I have some issues implementing the dual time stepping procedure and was hoping some experienced eyes can help me out. Suppose I want to solve the advection equation using a dual time stepping procedure, then I have

,

where and 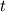are the pseudo and real time, respectively. Using first order (for simplicity) for all the derivatives, I get

.

I define the right-hand side (RHS) as



and then can rewrite the equation in explicit time integration form as

.

Once , where is some small (convergence number), the pseudo time derivative vanishes and i obtain the solution at the next time step. The pseudo code for my example follows below

while()
   while( and )
   
      Do i=2 to n
         
      End

      Do i=2 to n
         
      End

      calculate residual
      set iteration=iteration+1
      

   End

   
   

End

As long as I have the above code works fine, but as soon as I use different time steps, say , then my solution is off (by a factor of 2, in terms of propagated distance). It is probably an easy fix, but at the moment I am not quite sure what I am doing wrong.