 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
I am computing energy spectrum for computationally obtained turbulence data, which is statistically homogeneous in 2 directions (X & Z). The energy spectrum is calculated for a homogeneous plane, using Fourier transforms of the spatial data.
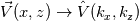 . . The calculated spectrum shows a 'bump' at higher wavenumbers (not the highest). It is prominent in a semilog plot (attached). I am wondering what could have resulted in this anomalous behaviour. I assume it is associated with some error in calculating the spectrum but has nothing to do with the physics. However, I am unable to find any error in the calculation. I would like to know if anybody in the community has encountered a similar erroneous spectrum, and what could cause such anomaly? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Uwe Pilz
Join Date: Feb 2017
Location: Leipzig, Germany
Posts: 744
Rep Power: 15  |
You may look whether the wavelength of your bump region coincides with the size of the mesh.
__________________
Uwe Pilz -- Die der Hauptbewegung überlagerte Schwankungsbewegung ist in ihren Einzelheiten so hoffnungslos kompliziert, daß ihre theoretische Berechnung aussichtslos erscheint. (Hermann Schlichting, 1950) |
|
|
|

|
|
|
|
|
#3 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
Hi piu58,
I should have mentioned my mesh and domain earlier.  There are 512x128 points in the XZ plane which has a physical dimension 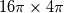 . Hence the maximum wavenumber for both . Hence the maximum wavenumber for both  is 32. The computed is 32. The computed 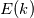 for various combinations of for various combinations of 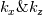 are binned in nearest integer values of are binned in nearest integer values of 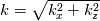 . As you suspected, the bump corresponds to . As you suspected, the bump corresponds to 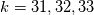 . . I understand that under-resolved data results in oscillations at highest wavenumbers.In this case, I am perplexed by the smooth spectrum beyond 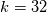 . .
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
What problem are you solving, a plane channel flow? And what about the Re_tau of your problem? what about y+ of the computed spectrum?
What I do not understand is the fact you have the spectrum extending over the Nyquist frequency... Or am I wrong in understanding your comment? Then, the magnitude of E(k) is very high, why? |
|
|
|

|
|
|
|
|
#5 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
The problem under consideration is temporal mixing layer.
On the x-axis I have 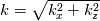 , which goes up till , which goes up till 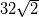 . That is why the spectrum extends beyond the Nyquist limit 32. However, I am unsure about the correctness of the same. . That is why the spectrum extends beyond the Nyquist limit 32. However, I am unsure about the correctness of the same.As of now, both k and E(k) are not scaled. My objective of plotting the spectrum is to make sure I am resolving the scales sufficiently. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
|
|
|
|

|
|
|
|
|
#7 | ||
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
Quote:
Quote:
To summarise, can I attribute the "bump" to the method where I am going above the Nyquist limit? |
|||
|
|

|
|||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Compute the 1d spectra but perform the spatial averaging along the normal direction
|
|
|
|

|
|
|
|
|
#9 | |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
Quote:
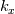 , and vice versa. In one of the threads in this forum, it is suggested that a Fourier transform is performed first and the coefficients are averaged. Is that the right way to do it? Or should I take average before transformation? , and vice versa. In one of the threads in this forum, it is suggested that a Fourier transform is performed first and the coefficients are averaged. Is that the right way to do it? Or should I take average before transformation?
|
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No, you compute first the FFT and then you perform the average of the coefficients |
||
|
|

|
||
|
|
|
#11 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
The calculated one-dimensional spectrum is attached.
A smooth curve is not obtained even after averaging FFT coefficients in the Z direction. Is it required to perform an average in time to obtain a smooth spectrum? |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
That looks quite correct ... have a look at sec.5.2 here
https://www.researchgate.net/publica...-uniform_grids and Ref.42 in the reference |
|
|
|

|
|
|
|
|
#13 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
One dimensional spectra,
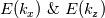 , calculated from the spatial data corresponding to center plane, are attached. Here I have binned them into integer values of , calculated from the spatial data corresponding to center plane, are attached. Here I have binned them into integer values of 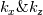 . .In this reference, the spectrum is calculated as 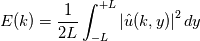 , ,which seems to be an averaging in the non-homogeneous direction. If so, what difference this makes to the spectrum? |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Your results seems physically acceptable.
You can have two choices: 1) the averaging along the non-homogeneous domain give the total energy content of the mixing layer for each wavenumber component. 2) computing and analysing spectra at several stations along y+. This is for example the standard procedure for a channel flow. Both are correct and the choice depends on what you want to analyse. I used the averaging along y to compare the solutions with the paper of Lesieur. |
|
|
|

|
|
|
|
|
#15 | ||
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
Dear FMDenaro,
Thank you for your valuable suggestions. Can you provide some clarification regarding the 'binning' procedure? Quote:
Quote:
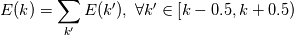
|
|||
|
|

|
|||
|
|
|
#16 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The plot is versus the frequency or the integer wavenumber, the relation being k=n*2*pi/L (n=0,1,2..,Nmax). The Nyquist frequency is kmax=pi/h. This is for each direction Lx and Lz.
What do you mean exactly for "binning procedure"? |
|
|
|

|
|
|
|
|
#17 |
|
Member
Aru
Join Date: Feb 2012
Location: Chennai, India
Posts: 40
Rep Power: 14  |
The length of the domain in x direction is
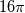 and has 512 points. A Fourier transform of this spatial data gives amplitudes of 256 frequencies (n=0,1...256). Corresponding wavenumbers are k=0,1/8,2/8.....,32 and they are not all integers. and has 512 points. A Fourier transform of this spatial data gives amplitudes of 256 frequencies (n=0,1...256). Corresponding wavenumbers are k=0,1/8,2/8.....,32 and they are not all integers. In the latter plot, I have used only integer values of wavenumber on the x-axis. The energy of non-integer wavenumbers is rounded off to nearest integer k. For example, E(1) is the sum of all u(k)^2 for k=4/8,5/8,.....,10/8,11/8. This procedure was described in a reference, but I couldn't trace it now. |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
After you perform the FFT, you have a vector of the complex Fourier coefficients for each integer n=0,1,... Thus, you can plot (in a log scale) the modulus versus these non-dimensional numbers or you simply convert the integers in the dimensional spatial frequency k = n*2*pi/L.
No "binning" in such procedure... |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How can I map the spectrum energy with its associated velocity field? | juliom | Main CFD Forum | 0 | March 23, 2016 09:16 |
| ATTENTION! Reliability problems in CFX 5.7 | Joseph | CFX | 14 | April 20, 2010 16:45 |
| turbulent energy spectrum | cfd.newbie | Siemens | 1 | June 20, 2008 00:48 |
| LES correlation and turbulent energy spectrum | Fabian | Main CFD Forum | 4 | October 18, 2005 03:04 |
| Energy Spectrum | Emad Khalifa | Main CFD Forum | 3 | June 30, 2003 17:03 |