 |
|
|
[Sponsors] | |||||
Flux discretization of 2D Compressible Navier-Stokes |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi all,
I am writing a solver for the 2D compressible Navier-Stokes equations in conservative form. When it is in conservative form it can be written as a 2D hyperbolic conservation law, but with a viscous flux. To start off simple, I would like to apply the Rusanov Flux (Local Lax Friedrichs) for my flux discretization, how I am unsure how to handle the viscous terms. A part of me wants to separate the fluxes and perform 2nd-order central differencing on the viscous terms and use a standard Rusanov flux for the advection terms, but that would not maintain conservative form. I have 2 books on solving the compressible Navier-Stokes, and both use MacCormack's method. Furthermore, it uses backward/forward differencing to achieve 2nd-order accuracy. Would I apply a similar approach when using the Local Lax Friedrichs on the viscous flux? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
For the spatial discretization of the viscous terms I suggest to use a central linear flux reconstruction. That would be second order accurate and it is in conservative form. Furthermore, a time integration like the Crank-Nicolson scheme would be suitable. |
||
|
|

|
||
|
|
|
#3 |
|
Member
Anh
Join Date: Sep 2014
Posts: 72
Rep Power: 12  |
For viscous term, It uses central scheme at i-1/2 and i+1/2 for x direction, similar for y direction
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
||
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Well, this is correct if you have a uniform grid and if mu is constant.
In general in a FV implementation you compute only the fluxes on all faces (and you have to compute also the integral of the flux) and then the sum gives the update. As a consequence, you work without assuming that the grid size is uniform and mu can be variable as happens in compressible flow when you can express the dependence on the temperature. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi FM Denaro,
Currently I am working under the assumption of constant mu and a uniform grid. Do you have any good references on the finite volume for non-uniform grids? Thanks, Selig |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
It is a general topic you can find in any good textbook about CFD. Start having a look to the book of Peric and Ferziger. Of course, differences appear if you work with non-uniform structured or unstructured grids. |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Non-uniform catesian grids are straightforward. You only need to calculate the local distances between cells and include that as a parameter (i.e. it's no longer
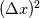 everywhere). You simply need to resist doing analytical simplifications. For example, as Filippo mentioned, don't do this thing where you put them together because the everywhere). You simply need to resist doing analytical simplifications. For example, as Filippo mentioned, don't do this thing where you put them together because the 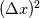 is going to depend on the local grid and don't also assume mu is constant. It also would have been more obvious that diffusive fluxes are conserved is going to depend on the local grid and don't also assume mu is constant. It also would have been more obvious that diffusive fluxes are conservedFor non-uniform grids (but still cartesian) few things change except you might want to tweak the the coefficients in your discretization schemes. But from a code-writing standpoint, that doesn't stop you. I.e. instead of [1 -2 1] for the diffusive term you might want to do [1.5 1.5 1] where the coefficients are related to the local cell distances. There is an intermediate step between uniform cartesian and a completely unstructured grid that I would recommend. That is the uniform (or non-uniform) structured grid but non-cartesian. I.e. instead of a bunch of rectangles or boxes that are aligned with coordinate system, you have a bunch of diamonds, trapezoids, parallelograms, or boxes that are misaligned with the coordinate. In this situation, the vector between two cell centers is mis-aligned with the derivatives in each direction. Now you have to keep track of the skewness angle of every cell face. Unstructured grids are similar. The challenge with unstructured grids, is you have to store cell connectivity data. For each cell, you need a way to figure out which cells are the neighboring cells. As soon as you skewed cells, you generally want to upgrade your method to calculate the cell gradients from a simple green-gauss method to what's commonly referred to as a least squares based method. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Filtered navier stokes equation..LES:: | Palani Velladurai | Main CFD Forum | 7 | September 6, 2013 03:51 |
| Adding a term to Navier Stokes Equation | ashtonJ | CFX | 3 | January 15, 2011 07:32 |
| Navier stokes compresible viscid flow fea, somebody can help? | Jose Choy | Main CFD Forum | 3 | October 24, 2003 03:28 |
| total mass flux correction for compressible fluid? | Francesco Di Maio | Main CFD Forum | 0 | August 21, 2000 05:23 |
| help: I am trying to solve Navier Stokes compressible and viscid flow | Jose Choy | Main CFD Forum | 2 | May 18, 2000 06:45 |