 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Ben
Join Date: Mar 2017
Posts: 1
Rep Power: 0  |
I'm hoping to build a FV Navier-Stokes solver for compressible pipe flow. The solver will be 2-D (r and z) and we are assuming no gradients in the theta direction and zero velocity in the theta direction. My question is: does it make a difference if I solve with 2-D cylindrical or 2-D cartesian coordinates and formulation of the Navier Stokes equation? If my mesh is 2-D in r and z, and the flow has no
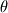 dependence, it seems that the cylindrical form should reduce to the cartesian form (because they can both equally describe my 2D mesh). But am I missing something essential? dependence, it seems that the cylindrical form should reduce to the cartesian form (because they can both equally describe my 2D mesh). But am I missing something essential?Thanks for your help -- I'm a beginning student of CFD (and even more so finite volumes) but having lots of fun. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
FV uses the weak form of the governing equation, so whether you start with x,y,z or r,theta,z as the basis for the strong form, it doesn't matter. You will integrate over finite volumes that are toruses with rectangular cross-sections. Your triple integrals will run from [r0 -> r1, z0 -> z1, 0 -> 2*pi]. If you start with x,y,z basis, you will likely have to transform variables to cylindrical to make the triple integral doable. There is really no differences. It comes down to either transforming the strong form to cylindrical coordinates and then doing easy FV integrals....or starting with the cartesian strong form, integrating over the same finite volumes and doing a "change of variables" in the integrals to make the simpler that end of being cylindrical coordinates.
The only real difference that I can think of can come from these two different formulations is how we do interpolation in the theta direction--and you don't have to worry about that. The cartesian treatment may lead to interpolation on 3D straight-lines connecting neighboring cell centroids. Using cylindrical coordinates logically leads to interpolation along circular arcs in the theta direction. This distinction is usually minor and sort of evaporates as soon as your meshes become unstructured. Good luck. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Unfortunately you cannot simply solve it in cartesian and do a coordinate transform.
A physical example of what you're doing is taking the solution for flow between parallel plates and claiming that flow between concentric pipes is the same! It's almost possible! In 2D, all the terms are identical between cartesian and cylindrical coordinates except for the radial-diffusion term. Imagine for a second that there is no diffusion, then it would not matter at all. But because of that one term, in general you don't get the same result. From a code-writing perspective: It is fairly trivial in FVM to switch from weak differential form of the gov. eqn. into the strong integral form. From the strong form, you can switch coordinates system by simply calculating the gradients a different way. Hence, a lot of commercial codes actually do use the strong form. In weak differential form it will look like your governing equations change. The reason for that change, is simply because your "gradient' has changed. You can easily take care of this also by properly introducing a weight function (1 for catesian, and r or 1/r for cylindrical) for radial diffusion term. You must solve them in the correct coordinate system, but it is pretty easy to do in 2D as long as you see it coming. Btw, one thing you need to watch out for is applying a limiter for the centerline (where r=0) when imposing the axis boundary condition. For a typical symmetry boundary condition one does not have to worry about the solution blowing up, but because of the singularity at r=0 in cylindrical space, you have to apply some damping. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
It is my old experience (many many years ago) that you can write a 3D FV code starting from the integral form of the equations and using Cartesian coordinates.
That allows also to avoid the singularity at r=0. For example, immagine a cylindrical FV surrounding the portion dz from r=0 to dr. You just need to compute the N fluxes from each of the faces at r=dr and theta=0,2pi of the volume. Then add the two fluxes from the upper and lower circles of area pi*dr^2. This way you have the value of the time dervative of the averaged variable. As you can see, no singularity occurs, the gradients are computed out from the r=0 axis. |
|
|
|

|
|
|
|
|
#5 |
|
Super Moderator
|
Quote:
https://github.com/cpraveen/nsc2ke The documentation explains the changes needed to make a usual 2d FV scheme to an axisymmetric one. |
|
|
|

|
|
 |
| Tags |
| cylindrical coordinates, finite volume method, navier stokes equations |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [General] Convert from Cartesian to Cylindrical | crashmaker | ParaView | 1 | June 12, 2015 19:51 |
| Converting cylindrical anisotropic diffusivity comonents into the cartesian setting | mcgintygs | OpenFOAM | 0 | January 29, 2014 09:47 |
| cylindrical coordinate vs cartesian coordinate | Lam | FLUENT | 10 | May 11, 2013 14:05 |
| 3D axisymmetric flow in cylindrical coordinate = 2D cartesian flow? | shubiaohewan | Main CFD Forum | 10 | May 2, 2013 15:08 |
| Transformation of a cartesian velocity gradient volTensorField to cylindrical coord. | alexey7783 | OpenFOAM | 5 | April 26, 2012 19:29 |