 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear all,
I have a question that I could not solve properly during the last years but which appears always somewhere. If I go through a lot of different CFD related books, we will find the shear-rate tensor to be defined as: 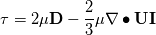 However, if we check out the shear-rate tensor in other literatures like in Bird et. al. we will probably find the following equation:  Where  is defined to be the bulk viscosity. This quantity is mentioned to be zero for monoatomic gases and does not play a big role for high dense gases and liquids. is defined to be the bulk viscosity. This quantity is mentioned to be zero for monoatomic gases and does not play a big role for high dense gases and liquids. So far so good. But however, I am interested in the definition of  and if the term and if the term  is the secondary viscosity is the secondary viscosity 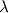 for Newtonian fluids for Newtonian fluids
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
||
|
|

|
|
|
|
|
#3 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
thanks for your reply. I think your number one represents the identity matrix, right? And the colon sign the double inner product of two matrices which is finally the trace. So I got what you wrote and you proofed that  . Just one thing that I never get (it is clear that we always can split a tensor in its deviatoric and hydrostatic part). . Just one thing that I never get (it is clear that we always can split a tensor in its deviatoric and hydrostatic part). Deformation rate tensor (strain-rate tensor) Deformation rate tensor (strain-rate tensor) is there a name for that? is there a name for that?You mentioned the volumetric viscosity. However Bird mentioned the bulk viscosity and based on your derivation it seems that the bulk viscosity is equal to 
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I try to give an explanation.
It can be shown that for a linear relation between stress and velocity gradient, the invariance to rotation and the symmetry of the tensor leads to write (Newtonian model): T = (-p +lambda* div v)*I +2 mu*D being lambda the second viscosity coefficient and I the identity tensor. Now, the tensor D can be decomposed according to D = I*trace(D)/3 +D0 =I*div v /3+D0 Now we can rewrite T = [-p +(lambda+2*mu/3)* div v]*I +2 mu*D0 = - phi*I +2 mu*D0 having defined the total dinamic pressure - phi = -p +(lambda+2*mu/3)*div v The definition of the bulk viscosity is k=(lambda+2*mu/3) Now, for divergence-free velocity, you get directly - phi = -p without any further assumption. When the velocity field produces a non vanishing divergence, you must consider the Stokes hypothesis k=0. |
|
|
|

|
|
|
|
|
#5 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
Thanks again. But again what is D0 and in your equations T should be the Cauchy stress tensor rather than the shear rate tensor (pressure is included). In addition, literature is welcomed. Sent from my HTC One mini using CFD Online Forum mobile app
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
It is the symmetric tensor having zero trace. It is a part of the general decomposition of a symmetric tensor in its isotropic and deviatoric parts. P.S.: yes, T is the Cauchy tensor That should be described here https://www.cambridge.org/core/books...621E80F9266993 |
||
|
|

|
||
|
|
|
#7 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
Quote:
|
|
|
|

|
|
|
|
|
#8 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hey,
thanks for the remark. That D0 is the deviatoric part was clear but I was just wondering if it has a special meaning like the deviatoric part of the Cauchy stress tensor is the shear rate tensor. Okay. Based on your explanation it is clear. Therefore, Bird et. al. is also wrong because if I set in the bulk viscosity  we get: we get: It should be correct. At last one question.   where  and and 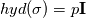 Based on the fact that the deviatoric part is traceless, the trace of the shear rate tensor is zero:  - right? - right?Therefore: 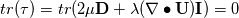 However, based on the fact that we split D again in its deviatoric part and hydrostatic part, it is not zero, right?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
yes it has a meaning, D0 contains only information about angular deformation of a volume of fluid, no increasing/decreasing of the volume.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#12 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
Hi,
I suggest you to look into Gurtin, The Mechanics and Thermodynamics of Continua, 2010 for more in-depht discussion of pressure and equilibrium pressure. By 7.1 you already split dev and hyd part of stress so "dev Cauchy = 2 mu D_O = 2 mu dev D". |
|
|
|

|
|
|
|
|
#13 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Thanks for your reply. Can it be that we need the term
 , to ensure that , to ensure that  gets traceless in order to fulfill eqn. (7.3). gets traceless in order to fulfill eqn. (7.3). However, I will look into the mentioned literature (hopefully it is available here).
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#15 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Okay ... things are sometimes not easy to explain (at least for me).
We split the Cauchy stress tensor in its deviatoric part and hydrostatic part. The deviatoric part is traceless. For tau wie have:  Right? Okay. Based on the fact that D is not traceless, we have to choose B in order to make the whole equation traceless again. Right? However, I think I have to check out the books / literature.
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; January 19, 2017 at 10:45. |
|
|
|

|
|
|
|
|
#16 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
You need to distinguish between incompressible and compressible fluid and also between equilibrium pressure and pressure. Also it seems that you have some misunderstanding about constitutive equation for Newtonian fluids. I have choosen A and B to point out that there is lot of misconception about second viscosity coefficient and bulk viscosity. It is usually written as
 where mu is first viscosity coefficient (dynamic viscosity) and lambda is second viscosity coefficient. In case of incompressible fluid, D=D_O and p=p_eq, hence  but in case of compressible fluid  ![{\boldsymbol{\sigma}} = - [ p_{eq} - (B + \frac{2}{3} A ) (\nabla \cdot \textbf{v}) ] {\bf 1} + 2 \mu {\bf D}_O {\boldsymbol{\sigma}} = - [ p_{eq} - (B + \frac{2}{3} A ) (\nabla \cdot \textbf{v}) ] {\bf 1} + 2 \mu {\bf D}_O](/Forums/vbLatex/img/4319d47dea352c865ee2a108f5e53dc5-1.gif) and  Now you can write dev Cauchy and hyd Cauchy where hyd Cauchy = "pressure". But the Cauchy stress tensor is usually split:  where T is viscous part of Cauchy stress tensor. And (total) pressure is 
Last edited by elones; January 19, 2017 at 16:37. |
|
|
|

|
|
|
|
|
#17 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
HI Ondřej,
thanks for you explanation. You are right, I am missing a few things for this topic but only based on the fact that I never saw the description in all of my literature. However, I will check out the literature given above on monday an I hope that after that I have a better understanding. Thanks for your explanation but I am still a bit confused based on my not deep insight into that topic. I will change it as soon as possible. Thank you very much.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Dynamic viscosity and Kinematic viscosity | asal | FLUENT | 7 | September 3, 2019 02:25 |
| Problem with divergence | TDK | FLUENT | 13 | December 14, 2018 07:00 |
| Ratio of eddy viscosity to molecular viscosity : Laminar or turbulent flow? | JuPa | CFX | 7 | September 9, 2013 08:45 |
| Too low temperature at combustor outlet | romekr | FLUENT | 2 | February 6, 2012 11:02 |
| External Flow Computations - Lift and Drag | Ramanath KS | Main CFD Forum | 9 | December 28, 2000 18:38 |