 |
|
|
[Sponsors] | |||||
[3D Vortex Particle Method]How to calculate velocity derivatives |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Youjiang Wang
Join Date: Apr 2015
Location: Hamburg
Posts: 22
Rep Power: 11  |
Now, I am trying to write a simple code about 3D Vortex Particle Method. However, when I dealing with the stretching term ((
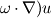 ), I face a problem. I don't know what's a good way to calculate the velocity derivatives. ), I face a problem. I don't know what's a good way to calculate the velocity derivatives.I am reading Cottet's book "Vortex Method: theory and practice". This problem is not explained explicitly, only be referred as a distribution way 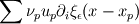 . It seems that, this formula regard the velocity in the same way with the vorticity. I mean, firstly concentrate it on particles, and then smooth it. . It seems that, this formula regard the velocity in the same way with the vorticity. I mean, firstly concentrate it on particles, and then smooth it.My idea is to apply the derivative operator directly on the velocity kern. I mean while velocity is got through  , can I calculate velocity derivatives by , can I calculate velocity derivatives by 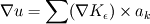 . . Thanks for any response. Thanks for any response.
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
adrin
Join Date: Mar 2009
Posts: 115
Rep Power: 17  |
differentiating the kernel K directly is what most people in the field do. I haven't read the book, but I suspect the smooth velocity approach (your first summation) might be related to the topic of formulating it to preserve the solenoidal nature of the vorticity transport equation (the original idea actually came from me during a discussion with Cottet). The smooth velocity approach does not work well.
adrin |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Youjiang Wang
Join Date: Apr 2015
Location: Hamburg
Posts: 22
Rep Power: 11  |
Thank you very much.
The smooth velocity approach is actually a method used to preserve the solenoidal nature of the vorticity. And it's used in a version of vorticity-in-cell methods as written in the Book. It's exciting to know the original idea came from you. |
|
|
|

|
|
 |
| Tags |
| 3d vortex particle, stretching, velocity derivative |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Calculate velocity components from shear stress | Arnoldinho | OpenFOAM Running, Solving & CFD | 0 | August 29, 2011 13:07 |
| Access to the particle position and velocity | Christoph_84 | OpenFOAM | 0 | September 30, 2010 10:58 |
| Variables Definition in CFX Solver 5.6 | R P | CFX | 2 | October 26, 2004 03:13 |
| Terrible Mistake In Fluid Dynamics History | Abhi | Main CFD Forum | 12 | July 8, 2002 10:11 |
| slip velocity on boundary (V.P.M) | Lee, Juhee | Main CFD Forum | 3 | October 22, 1998 16:30 |