 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
kiwi
Join Date: Mar 2012
Location: South East Asia
Posts: 58
Rep Power: 14  |
Dear all,
I have done the simulation with a nonnewtonian fluid, whereby the fluid pass through the a chamber(inlet as a velocity profile) and exit at the outlet tube(p=0). my simplified geometry is a rectangle connect to a tube. I found out that when the velocity gradient from the middle to the outlet increase, there is more wall shear stress on the wall. When the velocity gradient on the wall decrease , my result shows that there is less wall shear stress on the wall. I always thought that when the velocity gradient on the wall increase, the fluid will be less sticky , and move fluent, then reduce shear stress on the wall. But my results is opposite to my understanding. is there any mistake on results or my understanding? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 16  |
Hi, the behaviour of non-newtonian fluids is not unique. There are basically two kinds of non-newtonian fluids as far as I know: shear-thinning and shear-thickening.
- Shear-thinning: the shear stress decreases with the shear strain rate, i.e., the fluid becomes less "sticky" when it is subjected to high velocity gradients. An example of that would be ketchup, as soon as you shake the bottle it will flow easily downwards, otherwise it will stay attached to the walls of the bottle. - Shear-thickening: opposite behaviour, the shear stress increases with the shear strain rate. Think of a mixture of water and corn starch (check it on youtube and you will see many cool videos where you can see that when this fluid is subjected to high velocity gradients, it becomes almost like a solid, otherwise is pretty fluid). To sum up: you must check which kind of non-newtonian fluid shear stress vs shear strain rate law your CFD cose is using. Cheers. |
|
|
|

|
|
|
|
|
#3 | |
|
Member
kiwi
Join Date: Mar 2012
Location: South East Asia
Posts: 58
Rep Power: 14  |
Quote:
Thanks for your advice. so do you think that Carreau model which under velocity 0.0035m/s , will it have shear thickening effect? |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 16  |
Hi, I must admit that I did not know this model. A quick search shows that:
 The behaviour of your fluid will depend then on the value of the coefficient n: n>1: Viscosity increases with the shear strain rate ( 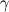 ), shear-thickening fluid. ), shear-thickening fluid.n=1: Viscosity is independent of shear strain rate, Newtonian fluid. n<1: Viscosity decreases with shear strain rate. Shear-thinning fluid. Notice that although the viscosity decreases, the shear stress still increases with the shear strain rate, as it is the product of viscosity times the shear strain rate, so it will increase slower than linearly with the shear strain rate. n<0: Assuming that 1<<(lambda*gamma)^2 and bearing in mind that shear stress=mu*gamma, the shear stress rate will actually decrease with the shear strain rate (i.e. velocity gradient). Can you check in your code which value of n is set, I think that is the key of the question. I guess that if you are observing and increase of shear stress with the velocity gradients it seems that your fluid is indeed shear-thickening. Cheers. |
|
|
|

|
|
|
|
|
#5 |
|
Member
kiwi
Join Date: Mar 2012
Location: South East Asia
Posts: 58
Rep Power: 14  |
Hi, Michujo,
Thanks for your explanation. Yup, i understand it, my one n<1. is belong to shear thinning behaviour. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| wall slip law for newtonian fluid | tsi07 | FLUENT | 0 | April 19, 2012 13:13 |
| Centrifugal Pump Cavitation problem or not. | ismael.s | CFX | 13 | February 27, 2012 09:00 |
| CFX results export problem ? | nasir | CFX | 2 | November 4, 2011 22:10 |
| Different fluid problem | prateek jain | CFX | 1 | May 3, 2007 10:11 |
| Symmetric problem - Assymetric results | Mark | Phoenics | 2 | July 2, 2001 10:04 |