 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
Hello to everyone!
I will describe my problem below as detail as possible. I need to calculate a 2D hypersonic flow (M=10.15, T=250 K) around this wedge (length dimension is mm): 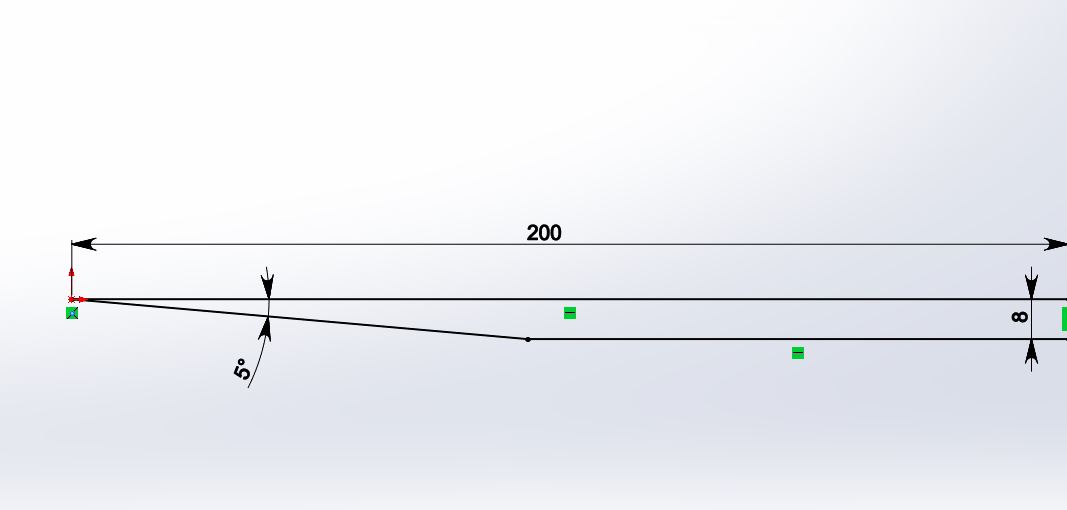 My thermal boundary conditions on the walls are: Tw (wall temperature)=540K, with this a have no problems. But I have problems with velocity conditions on the wall. First of all, I'd like to tell you, that simple "No slip" conditions (Ux=0 on the wall) don't work on such velocities (temperature near a "nose" is around 8000K, that is incorrect). So, I need to specify my gas velocity on the wall as 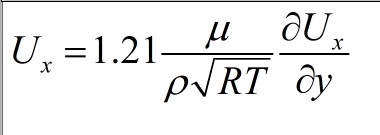 , where x is an axis along surface, and y is an axis, normal to it. , where x is an axis along surface, and y is an axis, normal to it. How can I do this in Fluent? SOLVED! For new problem (adding volume viscosity), please go below. Oleg Last edited by Oleg V.; November 8, 2014 at 12:41. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
Search in the help for low-pressure boundary slip. That comes close to what you want (and it might be exactly what you want).
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
pakk, thanks for your quick answer!
Where should I search for it? In Fluent help ---> "Boundary conditions"? |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
up to see more answers

|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
Your question already seems to be answered?
Just search in the help. You should learn how to do that, but for this case I can tell you that the answer is in Fluent Theory guide section 7.2.3. If you have more specific questions, ask them, but probably you'll need to do some work yourself before you can ask the right question. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
pakk,
Thank you sooo much! At thistime I am reading this section carefully, and then may be I will write more questions. Yeah, these species conditions look so similar to those, that I wrote, but I don't want to close this topic, because I didn't finish my work, sorry =) |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
pakk,
Boundary Condition, which are in 7.2.3 in Theory Guide, are exactly what I need. Now I try to understand, how can I do this in my case, because there are a lot of variables in this section. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
You want to have:
 In an ideal gas (which is an appropriate condition in low-pressure), you know that density  , with M the molar mass. So: , with M the molar mass. So: I now happen to recognize the viscosity-based definition of the mean free path:  So your equation becomes:  So all you have to do to match your equation to Fluent's equation, is choose alpha_v such that  By the way: your equation is dimensionally incorrect. That is why I get the annoying M in my result. You might want to check if the 1.21 in your equation is really dimensionless or should have unit, or maybe you made a mistake somewhere with the molar mass  . .
|
|
|
|

|
|
|
|
|
#9 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
pakk,
I have to correct, that R in my formula is specific gas constant (R=287 J kg−1 K−1), and then  . I did a mistake, that I didn't write it, sorry! . I did a mistake, that I didn't write it, sorry!If so, your formula for momentum accommodation coefficient is  . .Now I want to ask you, if I do steps correct: 1) I turn on "species transport" in "Models" and select "mixture-template" 2) then in Viscous I make a tick in "Laminar" and then in "Low-Pressure Boundary Slip" 3) I go to "Materials" , than I edit my mixture and in "Species" window I select only air  4) in my "air" in "mixture-template" I correct accommodation coefficient to which I need. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
Yes, those seem to be the steps. (Only 2 and 4 are specific for the slip.)
In retrospect, I should have noticed that you used the specific gas constant. I think it should be forbidden to use the specific gas constant. Before the relation between specific gas constant and molar masses was found, it was acceptable, but the last 200 years the specific gas constant should have been replaced everywhere by R/M. Just my opinion. 
|
|
|
|

|
|
|
|
|
#11 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
pakk,
Thank you very much for your help with slip conditions! And now about gas constant or specific gas constant. My opinion, that it's only a notation. For example, if I read a book or an article, I go to "notations" and read, that (for example) Tw is wall Temperature, and R is specific gas constant. I am studying aerodynamics, and in this science usually used specific gas constant. That's why I wrote my formula without any explanation. May be, that is because we usually use air, as a fluid material, and we know that R=287 for air and don't even think, that it is normal is gas constant / molar mass. It's not classical physics, it's more specific
 P.S. I have an article, in notation it is written: "R - gas constant", and in the text then they wrote "  " without any explanation. " without any explanation. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
You are right, it is only a notation.
But notation can be helpful or confusing. Calling temperature T and pressure p is helpful for (Western) people. Calling temperature p and pressure T would be confusing for (Western) people, even if it would be clearly explained in a "notation" section. Usually (I have no source for this but this is my experience), purely theoretical scientific progress is done in 4 steps (heavily simplified): 1. Something is discovered, and written down in a clumsy way because no good notation exists yet. ("If you take the sum of a number and a second number, and then add a third number, the result is the same as if you would first combine the second number and the third number, and then add the first number.") 2. Some notation is defined to simplify the statements. ("Let's call the first number a, the second number b, the third number b, and introduce the symbol + for sum, the symbol = for equality, and the brackets for operation order. The statement then simplifies to (a+b)+c=a+(b+c)." 3. From this simplified notation, the structure becomes more clear. People experiment with symbolic manipulation, and try to generalize the statement. ("Hey, we can do this with four numbers! ((a+b)+c)+d=a+(b+(c+d))). Or with multiplication! (a*b)*c=a*(b*c)." 4. Science progresses. If we would have to re-invent all notation, knowing what we know now, we would never introduce the specific gas constant. Knowing what we know now, we would introduce the universal gas constant (or even better: we would go to Planck units, and the universal gas constant would be 1, so we could ignore it). But this is offtopic 
|
|
|
|

|
|
|
|
|
#13 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
You gave a good example, but: usually for me M is Mach number, and R is specific gas constant. You wrote:
if you didn't write "M is the molar mass" may be I wouldn't understand you, because for me M is Mach. Problem? Problem  We don't have to re-invent, but everything must have it's limits. Small notations-yes, for everything ("+ means that it is sum of ... ") - no! As another example: you give a notation, that (physical quantity)  and then you write (for example) and then you write (for example)  . Because of that your equations become smaller and they look better to read and understand their physical sense. That's why we write . Because of that your equations become smaller and they look better to read and understand their physical sense. That's why we write  . It is simpler and you don't have to think about molar mass. . It is simpler and you don't have to think about molar mass.But we both know, that we won't change our opinion  P.S. It's hard to explain my thoughts in English, because it's not my motherlanguage, sorry!  P.P.S. Yeah, it's offtopic. My case will be calculated at night  If you want, I will add some pictures of the results =) But I am not sure, that everything will be right. If you want, I will add some pictures of the results =) But I am not sure, that everything will be right.
|
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
||
|
|

|
|
|
|
|
#15 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
Good evening!
Now I have new question for you. In Fluent Theory guide in Momentum Conservation Equations (Section 1.2.2.) is written: stress tensor 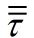 is given by is given by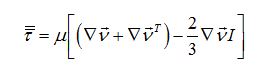 (1) (1)where 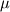 is molecular viscosity and I is the unit tensor. is molecular viscosity and I is the unit tensor. All I need is to modify this equation by adding volume viscosity (also called second viscosity or bulk viscosity)  or or 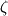 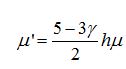 (2) (2)where 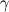 is adiabatic index and h=const. is adiabatic index and h=const. And then equation for stress tensor will be: 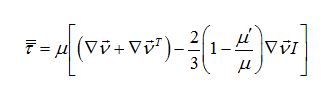 (3) (3) where 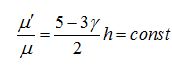 (4) (4)So, what I want is to modify equation (1) to (3) by adding a constant (4). Is there a simple way to do this? |
|
|
|

|
|
|
|
|
#16 |
|
New Member
Oleg Vlasov
Join Date: Oct 2014
Posts: 15
Rep Power: 12  |
no ideas?

|
|
|
|

|
|
 |
| Tags |
| hypersonic flow, slip velocity |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| sliding mesh problem in CFX | Saima | CFX | 46 | September 11, 2021 08:38 |
| Difficulty in calculating angular velocity of Savonius turbine simulation | alfaruk | CFX | 14 | March 17, 2017 07:08 |
| No results for solid domain | Gary Holland | CFX | 10 | March 13, 2009 04:30 |
| Concentric tube heat exchanger (Air-Water) | Young | CFX | 5 | October 7, 2008 00:17 |
| Simple Wall Boundary Conditions for Turb. Flow | Greg Perkins | Main CFD Forum | 4 | May 29, 2002 00:10 |