 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Join Date: Feb 2013
Posts: 30
Rep Power: 13  |
Hi everybody,
I'm simulating flow through porous media and it works well with FLUENT. However, I have a question concerning the theory behind the flow: Basically, two different formulations can be used, one is denominated the "superficial velocity formulation" and the other one is the "physical velocity formulation". In the superficial velocity formulation, a sink term is added the usual momentum equation, S = mu/alpha * v (in my model I neglect the inertia resistance) mu is the dynamic viscosity, v the velocity and alpha denotes the permeability. However, the solution changes (as it should) if I use different values for the porosity gamma. I now wonder where the porosity enters the model equations within the superficial velocity formulation? As far as I know, the permeability does not depend on the porosity, however, in the ANSYS FLUENT 12.0 Users-Guide - 7.2.3, I find the following statement: " Both K and C2 are functions of (1-gamma). " What kind of relation is that and how is it theoretically justified? Thank you for any piece of advice, Natalie |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
Since permeability refers to viscous losses, the nature of the porous medium will influence the value of alpha. Now naturally ,the "nature" here is inherently related with porosity
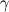 . .I will answer your question by taking a reference from Idelchik's handbook of hydraulic resistance, which is a widely accepted standard for hydraulic loss coefficients. Darcy's equation for a pressure drop in porous medium is given as: 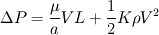 V here is a free stream velocity before the porous medium - or superficial velocity, 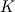 is coefficient of resistance and L is the length of porous medium. is coefficient of resistance and L is the length of porous medium.Idelchik generalises this pressure drop with linear and quadratic terms of V: 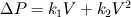 where 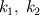 are empirical constants which can be understood easily from earlier equation. are empirical constants which can be understood easily from earlier equation. Now, intuitively, he defines pressure drop as: 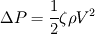 where, 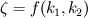 Thus Idelchik combines both viscous and inertial losses into 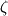 . .You will see that for different types of hydraulic resistances, he formulates the value of 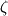 (unitless) as a function of percentage open area or porosity (unitless) as a function of percentage open area or porosity 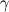 . He adds more terms for smaller Reynolds numbers, to account for viscous losses, thus implying that value of permeability should be influenced by porosity. . He adds more terms for smaller Reynolds numbers, to account for viscous losses, thus implying that value of permeability should be influenced by porosity. Incidently, I do observe that most of the analytical formulae he gives for 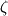 are functions of are functions of 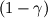 Obviously, in FLUENT, the values of C2 are per unit length, arrived by dividing 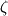 by the length of porous zone, and then incorporated in the momentum sink, as a pressure gradient and not as a pressure drop. by the length of porous zone, and then incorporated in the momentum sink, as a pressure gradient and not as a pressure drop.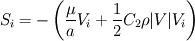 Hope this is useful. OJ |
|
|
|

|
|
|
|
|
#3 |
|
Member
Join Date: Feb 2013
Posts: 30
Rep Power: 13  |
So FLUENT does assume that the permeability depends on the porosity and modifies the value of 1/alpha accordingly?
Thanks for your answer, Natalie |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
OJ
Join Date: Apr 2012
Location: United Kindom
Posts: 473
Rep Power: 20  |
No, you have to set the value of permeability yourself as a part of your physics setup. FLUENT is just a solver, that solves your setup.
The gist of my post above was that both the permeability and inertial coefficient of resistance depend on porosity. OJ |
|
|
|

|
|
|
|
|
#5 |
|
Member
Join Date: Feb 2013
Posts: 30
Rep Power: 13  |
I understand, thank you!
Natalie |
|
|
|

|
|
|
|
|
#6 |
|
Member
Ftab
Join Date: Sep 2011
Posts: 87
Rep Power: 15  |
Dear Natalie and OJ,
I would appreciate if either of you would answer this issue. The original question of Natalie which led me also to this thread, is still not answered. Also defining Zeta and other coefficients would involve porosity, but ignoring the loss coefficient and making C2=0, will leave our momentum sinkterm as (miu/permeability)*Velocity. Assume that permeability is a constant number here. Why CFX is still asking for porosity? Why changing the porosity will change the simulation results as Natalie said, although it is not in our equations? Last edited by ftab; May 5, 2014 at 07:36. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
mohammadreza
Join Date: Jul 2015
Posts: 16
Rep Power: 11  |
Hi every body
I don't know how determine initial velocity for the flow in porous media. Thank you for time and consideration. Best regards |
|
|
|

|
|
|
|
|
#8 |
|
New Member
arman
Join Date: Feb 2016
Posts: 11
Rep Power: 10  |
hello
first: i want to say thank you for your guids about porous resistance .but i dont undrestant that how can i calcculet viscous and inertial resistans. secund :I am working on porpous media problem (heat transfer) but i cant find a good tutorial about heat transfer into porous media also i want to use source term in my problem. Thanks for your answer |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Porous Media Simulation with CFX/Fluent | Ghasem | ANSYS | 1 | May 14, 2013 10:07 |
| relative velocity resistance formulation, porous media | arminheidari | FLUENT | 0 | January 7, 2013 05:02 |
| compressible flow through porous media | Chirag2302 | FLUENT | 0 | March 3, 2012 00:13 |
| Discrete phase model in porous media | Pradeep | FLUENT | 0 | February 3, 2006 17:30 |
| porous media divergence | Phil | FLUENT | 0 | March 13, 2002 07:03 |