 |
|
|
[Sponsors] | |||||
Stokes second problem Upwind vs High Resolution |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
Hello,
I simulated a 2D case of an oscillating flat plate (Stokes second problem). Oscilating flat plate.png The setup of the simulation is made for unsteady state analysis, for a laminar flow (Reynolds number is 538). For plate movement, to the wall boundary condition of the flat plate I set an expression for velocity u, U = 0.1*cos( 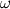 *t). *t).The frequency of the movement of the flat plate is 5 Hz. The time step is set to 0.002s (the Courant number is 32). The simulation time was set to 1s. The advection scheme was set to High Resolution and the transient scheme to Second order Backward Euler. I validated the results of the numerical simulation with the analytical solution of the problem: U = 0.1*exp(-y/ls)*cos( 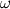 *t-y/ls), where ls = *t-y/ls), where ls =  (Stokes length) (Stokes length)When I compare the results of the simulation with the analytical solution I can see that the numerical simulation results are not in agreement with the analytical solution. Analytical solution vs numeric simulation 2nd order.png The RMS Residuals are around 10^-6 RMS Residuals 2nd order.jpg I tried another simulation where I change only the advection scheme to first order Upwind. The results from the numerical simulation improved when comparing with the analytical solution. Analytical solution vs numeric simulation upwind.png The RMS Residuals are also around 10^-6 RMS Residuals upwind.jpg Why the simulation results made with Upwind advection scheme are closer than the simulation results made with High Resolution scheme when comparing to the analytical solution? Shouldn't be more accurate the High Resolution scheme than the Upwind advection scheme? Any help is greatly appreciated! Ionut |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Thank you for describing your mathematical model in detail; however, you have no mentioned two very important aspects of a numerical simulation
1 - mesh size/quality --> Mesh independence 2 - timestep size --> Timestep independence Until you do not know if your solution is mesh and timestep independent, you cannot make any conclusions on the quality of the solution. You can say for "this mesh and timestep" the solution does not match, but that is the end of it. Once independent, you can then say - the converged mesh independent solution compares well/bad, with this much error, etc. Hope the above helps,
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
Thank you, Opaque.
Sorry for the late reply. 1 The mesh statistics (CFX Solver) Code:
+--------------------------------------------------------------------+ | Mesh Statistics | +--------------------------------------------------------------------+ | Domain Name | Orthog. Angle | Exp. Factor | Aspect Ratio | +----------------------+---------------+--------------+--------------+ | | Minimum [deg] | Maximum | Maximum | +----------------------+---------------+--------------+--------------+ | Flat_plate | 90.0 OK | 1 OK | 1 OK | +----------------------+---------------+--------------+--------------+ | | %! %ok %OK | %! %ok %OK | %! %ok %OK | +----------------------+---------------+--------------+--------------+ | Flat_plate | 0 0 100 | 0 0 100 | 0 0 100 | +----------------------+---------------+--------------+--------------+ I have reached to this size after a few tries generating the mesh for the simulation made with the time step of 0.002s where the results were independent of the mesh. 2 On the mesh for the time step of 0.002s I ran simulations with other time steps, starting from 0.2s to 0.00002s (I decreased the time step with 10 orders of magnitude every time) with corresponding Max Courant Number from 999.99 to 0.33. No difference in results was noticed after further decrease of time step 0.002s. Thank you for your time, Ionut |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
How many timesteps can you fit within one period of the boundary condition?
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
The period of the cosine wave is 0.2 seconds, I took a frequency of 5 Hz.
In one period, for a time step of 0.002 seconds, I would have 100 times steps. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Great.
Once you are around 100 timesteps per period, you should be fine for a simple sine/cosine wave. Going to higher time steps per period is usually for more complex flows where non-linearities start showing their ugly head. Now on the mesh normal to the wall, how many elements do you have between y = 0 and y = 0.0015 ?
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
Between y = 0 to y = 0.0015 I have 125 elements.
For the domain of 0.0048mx0.0036m I made a mesh of 399x299 elements. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Could you do the following?
1 - Plot the high resolution "Beta" coefficient for velocity vs y so we can see what the discretization is doing normal to the wall 2 - Run the simulation using Specified Blend Factor option, and the factor set to 0.75
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#9 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
I plotted the velocity u.beta for the High Resolution advection scheme simulation
Oscilating_flat_plate unsteady dt_0.002s U0_0.1 2xwidth u.beta_y.png and here is a zoom to the first figure, most of the time the advection scheme is a fully second order scheme Oscilating_flat_plate unsteady dt_0.002s U0_0.1 2xwidth u.beta_y zoom.png I made a simulation with the Specified Blend Factor of 0.75, the results are the same as the High Resolution scheme simulation Oscilating_flat_plate unsteady dt_0.002s U0_0.1 2xwidth SBF0.75.png I also tried the following: - simulation using the Specified Blend Factor of 1, which results in the use of the Central Difference Scheme. - simulation using the High Resolution scheme where as the initial conditions I used the simulation made with the Upwind scheme. All the above simulations give the same results as the High Resolution scheme simulation. It might be that the stokes second problem case can make the second order advection schemes give wrong results? Thank you, Ionut |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Well done!! It is great to see HighResolution is nearly 2nd order, and consistent with Specified Blend (0.75). Interesting is the fact that .beta minor drop is exactly at the maximum difference between the solutions.
I am as confused as you are. These are the only knobs that come to mind that you can play with 1 - Time step (checked) 2 - Mesh resolution (checked) 3 - Spatial discretization --> issue 4 - Boundary conditions (??) 5 - Convergence to periodic state (??) The comparison plot is done at t = t_final, correct? Could you please set a few monitor points at different heights normal to the wall? You can monitor Pressure and Velocity in the x,y directions (assuming that is the plane for the solution) When monitoring the solution in the ANSYS CFX Solver Manager, you can create a cyclic (for time-periodic problems), or polar plot of monitored variable vs time. A cyclic plot should repeat over itself if the solution has converged in time, and the polar plot should close perfectly at the end of each period. If the solution has not converged in time, the plots will continue drifting towards the periodic solution. A linear plot may be deceiving when the drift is small.
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#11 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
The comparison plot is made at the final simulation time, at 1s.
I will run the simulation again with monitor points for Pressure and Velocity and I will post them here when the simulation is completed. Thank you very much for your time, Ionut |
|
|
|

|
|
|
|
|
#12 |
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
Hi
I set three monitor points for velocity and pressure, at y = 0 m, y = 0.0005 m (at the maximum difference between the both solutions) and at y = 0.001 m. In this figure is shown the evolution for velocity at the monitoring points Oscilating_flat_plate unsteady dt_0.002s U0_0.1 2xwidth monitor_point velocity_u.jpg and in this figure is represented the evolution for pressure Oscilating_flat_plate unsteady dt_0.002s U0_0.1 2xwidth monitor_point press.jpg I forgot to mention that when I ran the simulation using the Upwind advection scheme, I used First Order Backward Euler for transient scheme. To see the influence of the transient scheme, I ran two more simulations: 1 High Resolution advection scheme and First Order Backward Euler transient scheme 2 Upwind advection scheme with Second Order Backward Euler transient scheme For case 1 the results are a little bit worse than the simulation using High Resolution and Second Order Backward Euler, and for case 2 the results are the same as the simulation using High Resolution and Second Order Backward Euler. In both cases the simulations converged in time, I checked using the polar plot in CFX Solver Manager. Thank you, Ionut |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Great!!
If I understood correctly, using SO Backward Euler the solutions for Upwind, Central Difference, and High Resolution are very close (nearly identical), correct? Based on that, would you agree that the favorable comparison between the Analytical solution the one using Upwind + FO Backward Euler was just a coincidence? One way to eliminate the time integration error for this case is to use the Harmonic Balance feature. You can do the following with your current setup 1 - Change the Analysis Type from Transient to Transient Blade Row 2 - Edit the Transient Blade Row panel, and change the Transient Method from Time Integration to Harmonic Balance 3 - Set the number of modes to 1 (the solution only has 1 harmonic) 4 - Set the Period to the period of interest 5 - I do not think you need to change anything else, and hopefully you do not get any pre-processing warnings/errors to worry about. 6 - Run the calculation with the default settings for Solver Control 7 - The monitor points in the Solver Manager should reach a flat line ~ the mean value of the variable within the period of interest If you expand the analytical solution such that you can write it as: Velocity = A cos (w * t) + B sin (w * t) you should be able to compare the Fourier Coefficients from the Harmonic Balance such that Velocity. Fourier Coefficient A0 = 0 Velocity. Fourier Coefficient B0 = 0 (always for any simulation) Velocity. Fourier Coefficient A1 = A (from expression you obtained above) Velocity. Fourier Coefficient B1 = B (from expression you obtained above) The differences between those coefficients should only be due to spatial discretization errors. The time approximation should be exact for this setup. Hope the above helps
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Erik
Join Date: Feb 2011
Location: Earth (Land portion)
Posts: 1,188
Rep Power: 23  |
Just a few clarification questions from your original post. Just trying to understand the problem:
If your time step is 0.002s, why are there more than 500 iterations in your model if you only simulated 1 second? How are you calculating Reynold's number? I get 166.7, not 583? Your stokes length is 0.24mm? And is that calculated using Hz or radians per second for omega? What is your kinematic viscosity? |
|
|
|

|
|
|
|
|
#15 | |||||||
|
New Member
G Ionut
Join Date: Sep 2016
Posts: 29
Rep Power: 10  |
Thank you for your help Opaque.
Quote:
Quote:
Quote:
I will try to install the latest version and run the simulation as you recommended. Hello Erik, thank you for helping me Quote:
Quote:
 , where U = 0.1 m/s, is the amplitude of the signal (maximum velocity in the cosine wave), L = 4.8 mm, is the length of the plate, , where U = 0.1 m/s, is the amplitude of the signal (maximum velocity in the cosine wave), L = 4.8 mm, is the length of the plate,  is the kinematic viscosity calculated as is the kinematic viscosity calculated as 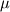 / /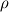 , , 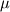 = 0.0008899 Pa*s and = 0.0008899 Pa*s and 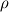 = 997 kg/m^3. The values for = 997 kg/m^3. The values for 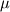 and and 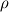 are the ones from CFX database. are the ones from CFX database.Quote:
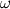 is calculated using Hz, is calculated using Hz, 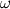 = 2* = 2*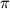 *signal frequency(Hz); ls = *signal frequency(Hz); ls =  . .Quote:
 = 8.9258e-07 m^2/s = 8.9258e-07 m^2/s
|
||||||||
|
|

|
||||||||
|
|
|
#16 | |
|
Senior Member
Join Date: Jun 2009
Posts: 1,880
Rep Power: 33  |
Quote:
Harmonic Balance has been available circa 2017/2018. Do not recall version numbers for those years.
__________________
Note: I do not answer CFD questions by PM. CFD questions should be posted on the forum. |
||
|
|

|
||
 |
| Tags |
| high resolution schemes, stokes second problem, upwind schemes |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| SU2-7.0.1 on ubuntu 18.04 | hyunko | SU2 Installation | 7 | March 16, 2020 05:37 |
| Changing from Upwind Scheme to High Resolution Scheme | AndreFecteau | CFX | 4 | March 1, 2019 18:40 |
| The resolution of the fluent interface is too high | aurelio | FLUENT | 0 | August 15, 2018 06:33 |
| Implementation of 2nd order upwind scheme | jaason | OpenFOAM Running, Solving & CFD | 4 | February 6, 2015 18:40 |
| larger blend factor or high resolution ? | amine | CFX | 2 | March 4, 2008 21:28 |