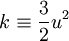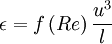Introduction to turbulence/Homogeneous turbulence
From CFD-Wiki
(Difference between revisions)
(→A first look at decaying turbulence) |
|||
| Line 24: | Line 24: | ||
</math> | </math> | ||
</td><td width="5%">(3)</td></tr></table> | </td><td width="5%">(3)</td></tr></table> | ||
| + | |||
| + | Now you can't get any simpler than this. Yet unbelievably we still don't have enough information to solve it. Let's try. Suppose we use the extanded ideas of Kolmogorov we introduced in Chapter 3 to related the dissipation to the turbulence energy, say: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | \epsilon = f \left( Re \right) \frac{u^{3}}{l} | ||
| + | </math> | ||
| + | </td><td width="5%">(4)</td></tr></table> | ||
Revision as of 09:25, 12 March 2008
A first look at decaying turbulence
Look, for example, at the decay of turbulence which has already been generated. If this turbulence is homogeneous and there is no mean velocity gradient to generate new turbulence, the kinetic energy equation reduces to simply:
|
| (1) |
This is often written (especially for isotropic turbulence) as:
|
| (2) |
where
|
| (3) |
Now you can't get any simpler than this. Yet unbelievably we still don't have enough information to solve it. Let's try. Suppose we use the extanded ideas of Kolmogorov we introduced in Chapter 3 to related the dissipation to the turbulence energy, say:
|
| (4) |

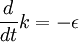
![\frac{d}{dt} \left[ \frac{3}{2} u^{2} \right] = - \epsilon](/W/images/math/a/c/2/ac251958c2df0a8a260f8f83d2645da2.png)