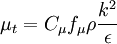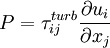Low-Re k-epsilon models
From CFD-Wiki
Revision as of 09:42, 14 May 2006
Contents |
Introduction
Good reviews of classical Low-Re k-epsilon models can be found in [Patel (1995)] and [Rodi (1993)]. There are hundreds of different low-Re k-epsilon models in the litterature. This article tries to summarize and describe the most common and classical models. Feel free to add more models here, but please only add models that have gained a widespread use in the CFD community.
Overview of models
The models presented presented here are:
| Model | Reference | Description |
| Chien Model | [Chien (1982}] | A very common model in turbomachinery applications. Has nice numerical properties. |
| Launder-Sharma Model | [Launder (1974)] | An old classical model which has attracted some attention for its ability to in model cases predict by-pass transition. |
| Nagano-Tagawa Model | [Nagano (1990)] | A model originally developed for heat-transfer applications. |
Governing equations
These models can be written in a general form like:
Where 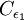 ,
, 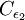 ,
, 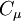 ,
, 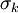 and
and 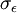 are model constants. The damping functions
are model constants. The damping functions 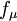 ,
, 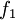 and
and 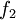 and the extra source terms
and the extra source terms 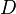 and
and 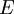 are only active close to solid walls and makes it possible to solve
are only active close to solid walls and makes it possible to solve 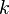 and
and  down to the viscous sublayer. Table below summarizes the constants, damping functions and boundary conditions for all k-epsilon models presented here.
down to the viscous sublayer. Table below summarizes the constants, damping functions and boundary conditions for all k-epsilon models presented here.
Model constants, daming functions and boundary conditions
| Chien | Launder-Sharma | Nagano-Tagawa | |
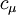 | 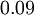 | 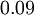 | 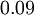
|
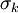 | 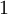 | 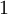 | 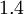
|
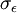 | 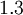 | 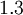 | 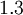
|
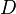 | 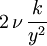 | 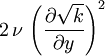 | 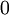
|
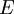 | 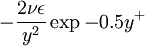 | 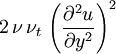 | 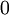
|
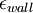 | 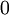 | 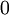 | 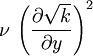
|
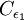 | 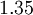 | 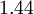 | 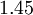
|
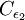 | 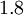 | 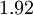 | 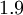
|
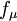 | 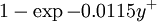 | 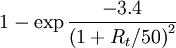 | 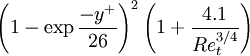
|
 |  |  | 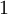
|
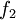 | 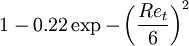 | 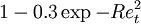 | 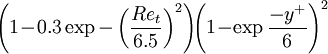
|
Where 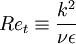 ,
, 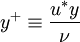 and
and 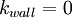 .
.
Performance, applicability and limitations
Not written yet
Implementation issues
Not written yet
References
Chien, K.-Y. (1982), "Predictions of Channel and Boundary-Layer Flows with a Low-Reynolds Number Turbulence Model", AIAA Journal, Vol. 20, No. 1, pp. 33-38.
Nagano, Y. and Tagawa, M. (1990), "An Improved k-epsilon Model for Boundary Layer Flows", Journal of Fluids Engineering, Vol. 112, pp. 33-39.
Patel, V. C. and Rodi, W. and Scheuerer, G. (1985), "Turbulence Models for Near-Wall and Low Reynolds Number Flows: A Review", AIAA Journal, Vol. 23, No. 9, pp. 1308-1319.
Rodi, W. and Mansour, N. N. (1993), "Low Reynolds Number k-epsilon Modeling with the Aid of Direct Simulation Data", Journal of Fluid Mechanics, Vol. 250, pp. 509-529.
Launder, B. E. and Sharma, B. I. (1974), "Application of the Energy-Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc", Letters in Heat and Mass Transfer, Vol. 1, No. 2, pp. 131-138.
Return to Turbulence modeling

![\frac{\partial}{\partial t} \left( \rho k \right) +
\frac{\partial}{\partial x_j}
\left[
\rho k u_j - \left( \mu + \frac{\mu_t}{\sigma_k} \right)
\frac{\partial k}{\partial x_j}
\right]
=
P - \rho \epsilon - \rho D](/W/images/math/8/d/7/8d787db6600e44ff6855992620431595.png)
![\frac{\partial}{\partial t} \left( \rho \epsilon \right) +
\frac{\partial}{\partial x_j}
\left[
\rho \epsilon u_j - \left( \mu + \frac{\mu_t}{\sigma_\epsilon} \right)
\frac{\partial \epsilon}{\partial x_j}
\right]
=
\left( C_{\epsilon_1} f_1 P - C_{\epsilon_2} f_2 \rho \epsilon \right)
\frac{\epsilon}{k}
+ \rho E](/W/images/math/5/b/d/5bdb9da87012a71cf28a70a9a0cd371f.png)