CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Gresho vortex

Gresho vortex

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
HannesGS (Talk | contribs)
(Created page with "== Classical Definition == The Gresho vortex was originally designed for incompressible flow, but here we consider the case of Euler equations. The Gresho problem [1] i...")
Newer edit →

Revision as of 07:33, 29 August 2013

Classical Definition

The Gresho vortex was originally designed for incompressible flow, but here we consider the case of Euler equations.

The Gresho problem [1] is a rotating vortex problem independent of time. Angular velocity 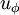u_{\phi} depends only on radius and the centrifugal force is balanced by the gradient of the pressure p.

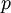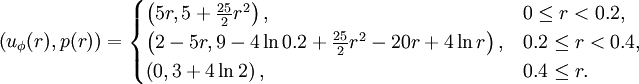
\left( u_{\phi}(r), p(r) \right) = \begin{cases} \left( 5r , 5 + \frac{25}{2} r^2 \right), & 0 \leq r < 0.2, \\ \left( 2-5r, 9 - 4 \ln 0.2 + \frac{25}{2} r^2 - 20 r + 4 \ln r \right), & 0.2 \leq r < 0.4, \\ \left( 0 , 3 + 4 \ln 2 \right), & 0.4 \leq r. \end{cases}

The radial velocity is zero and the density is one everywhere.


Dependence on Mach number

Miczek [2] modified the setup by introducing a reference Mach number. Pressure is scaled such that the rotation acts on this Mach number.

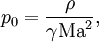
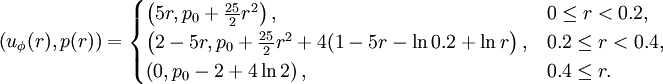
p_0 = \frac{\rho}{\gamma {\rm Ma}^2}, \left( u_{\phi}(r), p(r) \right) = \begin{cases} \left( 5r , p_0 + \frac{25}{2} r^2 \right), & 0 \leq r < 0.2, \\ \left( 2-5r, p_0 + \frac{25}{2} r^2 + 4 (1 - 5r -\ln 0.2 +\ln r \right), & 0.2 \leq r < 0.4, \\ \left( 0 , p_0 -2 + 4 \ln 2 \right), & 0.4 \leq r. \end{cases}

Now, we can use the Gresho vortex as test case how well the numerical scheme performs in dependence of the Mach number.


References

[1] Liska R., Wendroff B. Comparison of Several Difference Schemes on 1D and 2D Test Problems for the Euler Equations. SIAM J. Sci. Comput., 25(3), 995–1017 (23 pages).

[2] Miczek F. Simulation of low Mach number astrophysical flows. München, Technische Universität München, Diss., 2013.

[3] Happenhofer N., Grimm-Strele H., Kupka F., Löw-Baselli B., Muthsam H. A low Mach number solver: Enhancing applicability. Journal of Computational Physics Volume 236, 1 March 2013, Pages 96-118.

[4] Grimm-Strele H., Kupka F., Muthsam H. Curvilinear Grids for WENO Methods in Astrophysical Simulations. Submitted to Computer Physics Communications, 2013.


This article is a stub, a short article which needs to be improved. You can help by expanding it.
Retrieved from "https://cfd-online.com/Wiki/Gresho_vortex"
My wiki