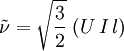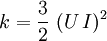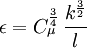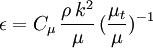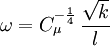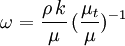Turbulence free-stream boundary conditions
From CFD-Wiki
Tohoughton (Talk | contribs) (→Dissipation rate) |
Tohoughton (Talk | contribs) (→From the turbulent length scale) |
||
| Line 47: | Line 47: | ||
The specific turbulent dissipation rate, <math>\omega</math>, can be computed using the following formulas: | The specific turbulent dissipation rate, <math>\omega</math>, can be computed using the following formulas: | ||
| - | ====From the | + | ====From the turbulence length scale==== |
:<math>\omega = C_\mu^{-\frac{1}{4}} \, \frac{\sqrt{k}}{l}</math> | :<math>\omega = C_\mu^{-\frac{1}{4}} \, \frac{\sqrt{k}}{l}</math> | ||
Revision as of 10:22, 15 May 2008
In most CFD simulations it is necessary to specify values of the turbulence variables at the inlets. For example, if you are using a 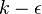 model you have to specify values of
model you have to specify values of 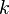 and
and  at the inlets. This is often difficult and a source of uncertainty since the incoming turbulence is rarely known exactly. Most often you are forced to make a more or less educated guess of the incoming turbulence.
at the inlets. This is often difficult and a source of uncertainty since the incoming turbulence is rarely known exactly. Most often you are forced to make a more or less educated guess of the incoming turbulence.
Estimating the turbulence model variables, like turbulent energy, dissipation or Reynolds stresses, directly is often difficult. Instead it is easier to think in terms of variables like the incoming turbulence intensity and turbulent length scale or eddy viscosity ratio. These properties are more intuitive to understand and can more easily be related to physical characteristics of the problem. For some guidelines on how these variables can be estimated see the respective CFD-Wiki page describing them.
Contents |
Formulas for computing the turbulence model variables
Once an appropriate turbulence intensity and turbulent length scale or eddy viscosity ratio has been estimated the primitive turbulence model variables can be computed from the following formulas:
Modified turbulent viscosity
The modified turbulent viscosity, 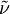 , can be computed using the following formulas:
, can be computed using the following formulas:
From the turbulence intensity and length scale
Where 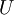 is the mean flow velocity,
is the mean flow velocity, 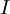 is the turbulence intensity and
is the turbulence intensity and 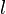 is the turbulent length scale.
is the turbulent length scale.
Ideally in the Spalart-Allmaras model 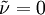 , but some solvers can have problem with that so
, but some solvers can have problem with that so 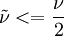 can be used. This is if the trip term is used to "start up" the model. A convenient option is to set
can be used. This is if the trip term is used to "start up" the model. A convenient option is to set 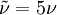 in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
Turbulent energy
The turbulent energy, 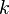 , can be computed as:
, can be computed as:
Where 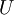 is the mean flow velocity and
is the mean flow velocity and 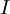 is the turbulence intensity.
is the turbulence intensity.
Dissipation rate
The turbulent dissipation rate,  , can be computed using the following formulas:
, can be computed using the following formulas:
From the turbulence length scale
Where 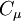 is a turbulence model constant which usually has a value of
is a turbulence model constant which usually has a value of 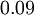 ,
, 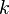 is the turbulent energy and
is the turbulent energy and 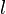 is the turbulent length scale
is the turbulent length scale
From the eddy viscosity ratio
Where 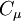 is a turbulence model constant which usually has a value of
is a turbulence model constant which usually has a value of 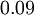 ,
, 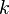 is the turbulent energy,
is the turbulent energy, 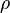 is the density,
is the density, 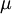 is the molecular dynamic viscosity and
is the molecular dynamic viscosity and 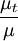 is the eddy viscosity ratio.
is the eddy viscosity ratio.
Specific dissipation rate
The specific turbulent dissipation rate, 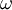 , can be computed using the following formulas:
, can be computed using the following formulas:
From the turbulence length scale
Where 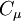 is a turbulence model constant which usually has a value of
is a turbulence model constant which usually has a value of 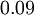 ,
, 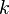 is the turbulent energy and
is the turbulent energy and 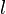 is the turbulent length scale
is the turbulent length scale
From the eddy viscosity ratio
Where 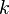 is the turbulent energy,
is the turbulent energy, 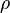 is the density,
is the density, 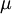 is the molecular dynamic viscosity and
is the molecular dynamic viscosity and 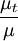 is the eddy viscosity ratio.
is the eddy viscosity ratio.