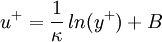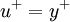Law of the wall
From CFD-Wiki
(Difference between revisions)
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
In the log layer the velocity profile can be estimated with the log law: | In the log layer the velocity profile can be estimated with the log law: | ||
| - | :<math>u^+ = \frac{1}{\kappa} \, ln(y^+) + | + | :<math>u^+ = \frac{1}{\kappa} \, ln(y^+) + B</math> |
| + | |||
| + | and close to the wall in the viscous sublayer | ||
| + | |||
| + | :<math>u^+ = y^+</math> | ||
Where: | Where: | ||
| Line 13: | Line 17: | ||
|<math>\kappa</math> || von Karman's constant (<math>\approx 0.41</math>) | |<math>\kappa</math> || von Karman's constant (<math>\approx 0.41</math>) | ||
|- | |- | ||
| - | |<math> | + | |<math>B</math> || Constant (<math>\approx 5.1</math>) |
|} | |} | ||
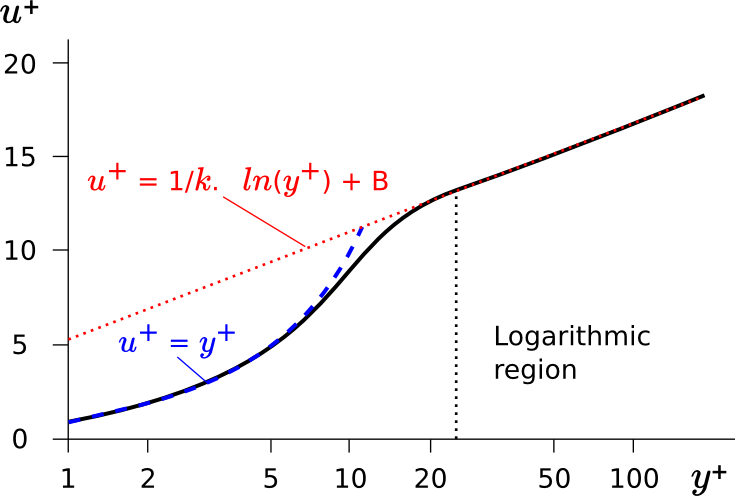
''We should have a lin-log plot here of a typical turbulent boundary layer to illustrate where the log-law is valid, anyone have one handy?'' | ''We should have a lin-log plot here of a typical turbulent boundary layer to illustrate where the log-law is valid, anyone have one handy?'' | ||
| + | |||
| + | In the image y is replaced with the letter n. | ||
| + | |||
| + | [[Image:Img_lawOfTheWall_whiteBG.png]] | ||
{{stub}} | {{stub}} | ||
Latest revision as of 08:32, 7 September 2011
In the log layer the velocity profile can be estimated with the log law:
and close to the wall in the viscous sublayer
Where:
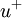
Dimensionless velocity 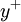
Dimensionless wall distance 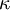
von Karman's constant ( 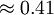 )
)
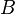
Constant ( 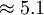 )
)
We should have a lin-log plot here of a typical turbulent boundary layer to illustrate where the log-law is valid, anyone have one handy?
In the image y is replaced with the letter n.