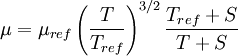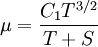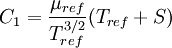Sutherland's law

From CFD-Wiki

(Difference between revisions)

Revision as of 17:20, 17 May 2007

In 1893 William Sutherland, an Australian physicist, published a relationship between the dynamic visocity, 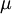$\mu$ , and the absolute temperature, 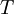$T$ , of an ideal gas. This formula, often called Sutherland's law, is based on kinetic theory of ideal gases and an idealized intermolecular-force potential. Sutherland's law is still commonly used and most often gives fairly accurate results with an error less than a few percent over a wide range of temperatures. Sutherland's law can be expressed as:

$\mu = \mu_{ref} \left( \frac{T}{T_{ref}} \right)^{3/2}\frac{T_{ref} + S}{T + S}$

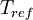$T_{ref}$ is a reference temperature.

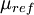$\mu_{ref}$ is the viscosity at the 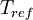$T_{ref}$ reference temperature

S is the Sutherland temperature

Some authors instead express Sutherland's law in the following form:

$\mu = \frac{C_1 T^{3/2}}{T + S}$

Comparing the formulas above the 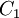$C_1$ constant can be written as:

$C_1 = \frac{\mu_{ref}}{T_{ref}^{3/2}}(T_{ref} + S)$

Sutherland's law coefficients:
Gas	$\mu_0 [\frac{kg}{m s}]$	$T_0 [K]$	$S [K]$	$C_1 [\frac{kg}{m s K ^ {0.5}}]$
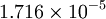
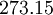
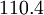
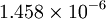
Air	$1.716 \times 10^{-5}$	$273.15$	$110.4$	$1.458 \times 10^{-6}$

References

Sutherland, W. (1893), "The viscosity of gases and molecular force", Philosophical Magazine, S. 5, 36, pp. 507-531 (1893).

@@ Line 15: / Line 15: @@
 :<math>C_1 = \frac{\mu_{ref}}{T_{ref}^{3/2}}(T_{ref} + S)</math>
-{| align=center border=1
+{| align=left border=2
-|+ Sutherland's law coefficients
+|+ Sutherland's law coefficients:
 ! Gas !! <math>\mu_0 [\frac{kg}{m s}]</math> !! <math>T_0 [K]</math> !! <math>S [K]</math> !! <math>C_1 [\frac{kg}{m s K ^ {0.5}}]</math>
 |-

Sutherland's law

From CFD-Wiki

Revision as of 17:20, 17 May 2007

References

Views

My wiki

wiki navigation

wiki search

wiki toolbox