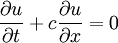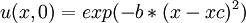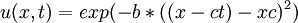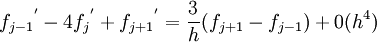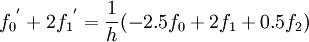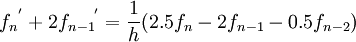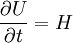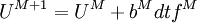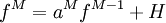Wave propagation
From CFD-Wiki
(Difference between revisions)
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| - | The 1-D wave propagation problem is used as a test case for studying the dissipation and dispersion errors in a given finite difference scheme.There are a number of schemes which can be used to solve the problem. The usage of a higher order compact stencil with a low storage 4th order Runge-Kutta scheme to solve the current problem is discussed. | + | The 1-D wave propagation problem is used as a test case for studying the dissipation and dispersion errors in a given finite difference scheme.There are a number of schemes which can be used to solve the problem. The usage of a higher order compact stencil (4th order considered here) with a low storage 4th order Runge-Kutta scheme to solve the current problem is discussed. |
| + | |||
| + | ==Governing Equation== | ||
| + | :<math> \frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x}=0 </math> | ||
| + | |||
| + | ==Initial Condition== | ||
| + | :<math> u(x,0)=exp(-b*(x-xc)^2)</math> | ||
| + | |||
| + | ==Exact Solution == | ||
| + | :<math> u(x,t)=exp(-b*((x-ct)-xc)^2)</math> | ||
== Compact scheme == | == Compact scheme == | ||
| + | :<math>{f_{j-1}}^{'}-4{f_j}^{'}+{f_{j+1}}^{'}=\frac{3}{h}(f_{j+1}-f_{j-1})+0(h^4)</math> | ||
| + | At Boundaries | ||
| + | :<math>{f_0}^{'}+2{f_1}^{'}=\frac{1}{h}(-2.5f_0+2f_1+0.5f_2)</math> | ||
| + | :<math>{f_n}^{'}+2{f_{n-1}}^{'}=\frac{1}{h}(2.5f_n-2f_{n-1}-0.5f_{n-2})</math> | ||
| + | |||
== Runge-Kutta == | == Runge-Kutta == | ||
Latest revision as of 07:19, 12 November 2005
Contents |
Introduction
The 1-D wave propagation problem is used as a test case for studying the dissipation and dispersion errors in a given finite difference scheme.There are a number of schemes which can be used to solve the problem. The usage of a higher order compact stencil (4th order considered here) with a low storage 4th order Runge-Kutta scheme to solve the current problem is discussed.
Governing Equation
Initial Condition
Exact Solution
Compact scheme
At Boundaries
Runge-Kutta
Consider
The low storage scheme is implemented as follows
where M refers to the stages ,dt is the time step and the coefficients a and b are given by
- a[5]={0,-0.41789047,-1.19215169,-1.69778469,-1.51418344}
- b[5]={0.149665602,0.37921031,0.82295502,0.69945045,0.15305724}
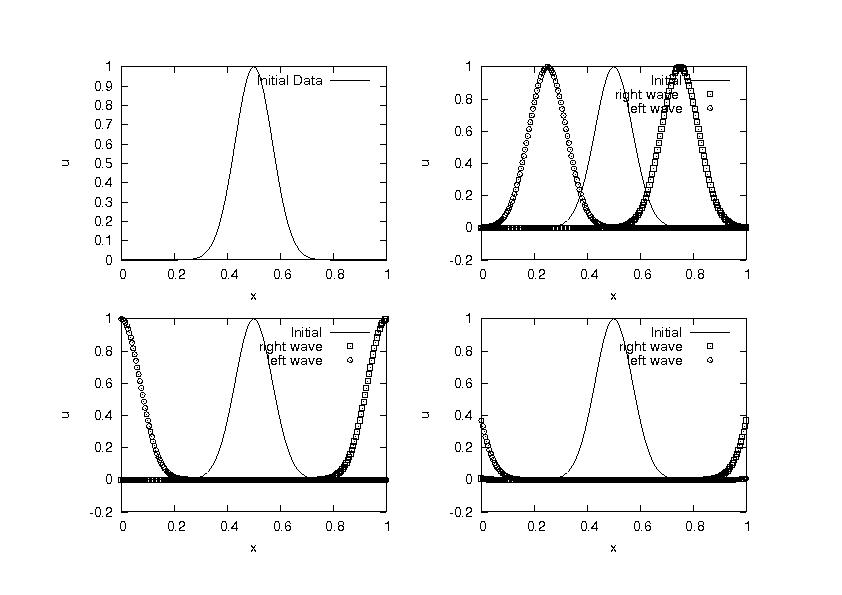
Sample result
Reference
- Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
- Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.