Incomplete Cholesky Factorization
From CFD-Wiki
(Difference between revisions)
| Line 15: | Line 15: | ||
</math> <br> | </math> <br> | ||
From this we can easily obtain<br> | From this we can easily obtain<br> | ||
| + | |||
| + | '''for := 1 step 1 until N do''' <br> | ||
| + | |||
<math> | <math> | ||
L_{ii} = \left( {a_{ii} - \sum\limits_{k = 1}^{i - 1} {L_{ik}^2 } } \right)^{{1 \over 2}} | L_{ii} = \left( {a_{ii} - \sum\limits_{k = 1}^{i - 1} {L_{ik}^2 } } \right)^{{1 \over 2}} | ||
| Line 22: | Line 25: | ||
L_{ji} = {1 \over {L_{ii} }}\left( {a_{ij} - \sum\limits_{k = 1}^{i - 1} {L_{ik} L_{jk} } } \right) | L_{ji} = {1 \over {L_{ii} }}\left( {a_{ij} - \sum\limits_{k = 1}^{i - 1} {L_{ik} L_{jk} } } \right) | ||
</math> ; where j = i+1, i+2, ..., N <br> | </math> ; where j = i+1, i+2, ..., N <br> | ||
| - | + | ||
| + | '''end (i-loop)''' <br> | ||
Revision as of 06:42, 14 September 2005
Cholesky Factorization
When the square matrix A is symmetric and positive definite then it has an efficient triangular decomposition. Symmetric means that aij = aji for i,j = 1, ... , N. While positive definite means that
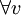
In cholesky factorization we construct a lower triangular matrix L whose transpose LT can itself serve as upper triangular part.
In other words we have
L 
LT = A
Algorithm for full matrix A
We have by definition
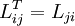
From this we can easily obtain
for := 1 step 1 until N do
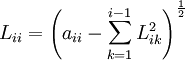
and
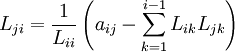; where j = i+1, i+2, ..., N
end (i-loop)
