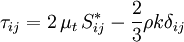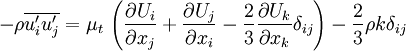Boussinesq eddy viscosity assumption
From CFD-Wiki
(Difference between revisions)
(→References) |
m (Reverted edits by Jabler (talk) to last revision by AlmostSurelyRob) |
||
| Line 39: | Line 39: | ||
{{stub}} | {{stub}} | ||
| - | |||
Revision as of 12:52, 15 November 2011
In 1877 Boussinesq postulated[1][2] that the momentum transfer caused by turbulent eddies can be modeled with an eddy viscosity. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity. The Boussinesq assumption states that the Reynolds stress tensor,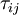 
, is proportional to the trace-less mean strain rate tensor, 
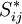, and can be written in the following way:
Where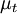 
is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
Note that for incompressible flow:
The Boussinesq eddy viscosity assumption is also often called the Boussinesq hypothesis or the Boussinesq approximation.
See also
References
- ↑ Boussinesq, J. (19877), "Essai sur la théorie des eaux courantes", Mémoires présentés par divers savants à l'Académie des Sciences 23 (1): 1-680
- ↑ Schmitt, F.G. (2007), "About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity", Comptes Rendus Mécanique 335 ((9-10)): 617-627
