 |
|
|
[Sponsors] | |||||
About boundary condition in FVM solid mechanics |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
JunSeok Oh
Join Date: Jun 2021
Posts: 1
Rep Power: 0  |
Hi, I'm currently working on computational solid mechanics using the finite volume method, specifically cell-centered FVM.
I've been working in the CFD field for a while, but I'm new to the CSM field, so I'm having trouble implementing boundary conditions. The discretized governing equation without body force and stabilization term is as follows: 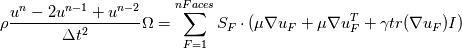 where 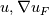 represent displacement vector and displacement tensor(or jacobian?) at the target face respectively. represent displacement vector and displacement tensor(or jacobian?) at the target face respectively.My code calculates the displacement gradient through the least square method. To obtain the LSM coefficient on the cell right next to the boundary, I've adopted the concept of "ghost points." These ghost points, which also have displacement values, are not used in the calculation directly but only used to calculate the displacement gradient. Boundary conditions are enforced by directly replacing the surface stress in the above equation. However, this approach has problems with rigorously defining the boundary conditions, both displacement, and traction. For traction (or Neumann) boundary conditions, the boundary surface stress can be clearly defined, but not the displacement of the ghost points. This can be problematic because the displacement gradient of cells adjacent to the boundary must also be calculated to be consistent with the traction boundary value. * This traction -> displacement conversion seems impossible? For displacement (or Dirichlet) boundary conditions, the displacement value of the ghost points can be clearly defined, but not the boundary surface stress. As a result, I can't directly replace the surface stress in the discretization. I haven't found anything in the literature I've searched so far that clearly addresses these issues. My current 'crude' solution to these problems is as follows: for traction BC, I simply extrapolate the displacement value of adjacent cells into ghost points, regardless of its traction value, and for displacement BC, I calculate the gradient of adjacent cells and assume this value as the boundary face displacement gradient, rather than directly replacing the surface stress. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| sliding mesh problem in CFX | Saima | CFX | 46 | September 11, 2021 08:38 |
| CFD analaysis of Pelton turbine | amodpanthee | CFX | 31 | April 19, 2018 19:02 |
| Boundary condition for solid region at inlet | selvam2487 | CFX | 1 | May 15, 2013 04:21 |
| CFX fails to calculate a diffuser pipe flow | shenying0710 | CFX | 7 | March 26, 2013 05:13 |
| RPM in Wind Turbine | Pankaj | CFX | 9 | November 23, 2009 05:05 |