 |
|
|
[Sponsors] | |||||
|
|
|
#61 | |
|
Senior Member
Daniel
Join Date: Mar 2013
Location: Noshahr, Iran
Posts: 348
Rep Power: 21  |
Quote:
Well I'm interested     Would you please share your findings? I'm trying to do the exact same thing. Regards |
||
|
|

|
||
|
|
|
#62 |
|
New Member
saeedbd
Join Date: Feb 2015
Posts: 6
Rep Power: 11  |
Hi foamers,
I am working on CompressibleInterFoam. I want to convert the T equation to a general energy conservation equation to remove some assumptions in the solver. Could you finally manage the energy equation? Assuming the perfectGas and perfectFluid Eos, we have e=Cv*T for each phase where e is internal energy. So, I am replacing T with et/(Cv_water Y_water + Cv_air Y_air) in the solver (et is the total internal energy with et = e1*Y1 + e2*Y2. But it gives me wrong results for bubble collapse case. So in fact, the T equation in original solver is as: Code:
fvScalarMatrix TEqn
(
fvm::ddt(rho, T) + fvm::div(rhoPhi, T) - fvm::Sp(contErr, T)
- fvm::laplacian(turbulence.alphaEff(), T)
+ (
fvc::div(fvc::absolute(phi, U), p)()() // - contErr/rho*p
+ (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()() - contErr*K
)
*(
alpha1()/mixture.thermo1().Cv()()
+ alpha2()/mixture.thermo2().Cv()()
)
==
fvOptions(rho, T)
);
and now is converted to Code:
fvm::ddt(rho, et) + fvm::div(rhoPhi, et) - fvm::Sp(contErr, et)
- fvm::laplacian(turbulence.alphaEff(), et)
+ (
fvc::div(fvc::absolute(phi, U), p)()()
// - contErr/rho*p
+ (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()() - contErr*K
)
*(
alpha1()/mixture.thermo1().Cv()() + alpha2()/mixture.thermo2().Cv()()
)
*(
Y1*mixture.thermo1().Cv()()+Y2*mixture.thermo2().Cv()()
)
==
fvOptions(rho, et)
where Y is the mass fraction: et=Y1*e1 + Y2*e2 and e1=Cv1*T , e2=Cv2*T. Also, I tried: Code:
fvm::ddt(rho, et) + fvm::div(rhoPhi, et) - fvm::Sp(contErr, et)
- fvm::laplacian(turbulence.alphaEff(), et)
+ (
fvc::div(fvc::absolute(phi, U), p)()()
// - contErr/rho*p
+ (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()() - contErr*K
)
==
fvOptions(rho, et)
But it does not work properly as well. The temperature drops at the interface immediately. In more details, I don't know why et in the new energy equation remains constant while I checked that we have velocity and K is NOT zero! (How can it be possible?) Then, after a very small time step 10^-12, since we have Y_water = 0.1 in the gas side of the interface, Temperature drops suddenly according to T = et/(Cv_water*Y_water + Cv_air*Y_air). The last point, it gives good results for the shock tube case which is not very dependent on temperature and energy. Do you know how to solve the issue? Thank you for your time. Saeed, |
|
|
|

|
|
|
|
|
#63 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
so I am not familiar with the solver you are using and I am also not familiar with its equation. However, VOF solves only one question for energy/momentum and so on. Just one question, you are solving for the field et, which is what? An energy right, the total internal energy. So, how do you transform the energy back into the temperature? I cannot see anything here. Because, as you are not solving for T anymore, the T field should stay constant. So actually, what you have to do is:
Hope this might help. Tobi
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#64 |
|
New Member
saeedbd
Join Date: Feb 2015
Posts: 6
Rep Power: 11  |
Hi Tobi,
Thank you very much for giving your feedback. Regarding the Temperature, I am obtaining it within the T = et/(Cv_water*Y_water + Cv_air*Y_air) equation which is based on perfectFluid and perfectGas. So to put it into a nutshell, I initialize the system with et=e1Y1+e2*Y2 and then solve the et equation. Then I update the T, based on the new et using the above equation. Best, |
|
|
|

|
|
|
|
|
#66 |
|
New Member
saeedbd
Join Date: Feb 2015
Posts: 6
Rep Power: 11  |
Yes with the considered EoSs.
I found an issue with the defined tolerance for et. So now it is being solved and this problem "I don't know why et in the new energy equation remains constant" is solved. |
|
|
|

|
|
|
|
|
#67 |
|
New Member
Zhongqi Zuo
Join Date: May 2018
Location: China
Posts: 8
Rep Power: 8  |
Hi openFoamers,
Thanks for your great discussion, it really helps a lot. However, when I look through the code, I find this term very confusing to me Code:
p_rghEqnComp1 & p_rgh But as I know & is "inner product", the operator is redefined in fvMatrix.C. p_rghEqnComp1 is a fvMatrix, p_rgh is a scalar field, how can the term be interpreted as Dp/Dt? Anybody can help? Thanks a lot. Zuo |
|
|
|

|
|
|
|
|
#68 |
|
Member
Join Date: Feb 2020
Posts: 90
Rep Power: 6  |
Hello to all,
I am also trying to understand the formulation of compressibleInterFoam for OpenFOAM ESI. However, the formulation is not clear to me. I would like to request a further clarification on the formulation of compressibleInterFoam. From the paper of Miller et al [1], previously referred to in this post, the pressure equation should be: ![\left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial P}{\partial t} + \vec{v} \cdot \nabla P\right ] + \nabla \cdot \vec{v}=0 \left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial P}{\partial t} + \vec{v} \cdot \nabla P\right ] + \nabla \cdot \vec{v}=0](/Forums/vbLatex/img/2f852cf70af2db9ff354d19ccd299d92-1.gif) Or, to better use the divergence theorem: ![\left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right] + \nabla \cdot \vec{v}=0 \left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right] + \nabla \cdot \vec{v}=0](/Forums/vbLatex/img/866657dbd5cbdcfc4780fbe48030aa91-1.gif) With the last term on the lefh hand side,  , we create a incompressiblePEqn and with the remainder terms a compressiblePEqn. , we create a incompressiblePEqn and with the remainder terms a compressiblePEqn.I took a look into the compressibleInterFoam from foam-exted. The pEqn.H has: An incomplete CompressiblePEqn written as: Code:
if (pimple.transonic())
{
pEqnComp =
(fvm::ddt(p) + fvm::div(phi, p) - fvm::Sp(fvc::div(phi), p));
}
else
{
pEqnComp =
(fvm::ddt(p) + fvc::div(phi, p) - fvc::Sp(fvc::div(phi), p));
}
![\left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right] \left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right]](/Forums/vbLatex/img/4042e372e99a522d306198f3d285e145-1.gif) The incompressiblePEqn which is derived by substituting the cell center velocity from the momentum equation. Code:
fvScalarMatrix pEqnIncomp
(
fvc::div(phi)
- fvm::laplacian(rUAf, p)
);
Code:
solve
(
(
max(alpha1, scalar(0))*(psi1/rho1)
+ max(alpha2, scalar(0))*(psi2/rho2)
)
*pEqnComp()
+ pEqnIncomp
);
![\left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right] + \nabla \cdot \vec{v}=0 \left ( \frac{\alpha_1 \psi_1}{\rho1}+\frac{\alpha_2 \psi_2}{\rho2} \right )\left [ \frac{\partial p}{\partial t} + \nabla \cdot \left ( p \vec{v} \right) - p \left ( \nabla \cdot \vec{v} \right) \right] + \nabla \cdot \vec{v}=0](/Forums/vbLatex/img/0bb8167f7d03373d32a3582df96a0424-1.gif) After solving the pressure equation, a dgdt term is updated with: Code:
dgdt =
(pos(alpha2)*(psi2/rho2) - pos(alpha1)*(psi1/rho1))
*(pEqnComp & p);
 Here are my questions: 1º Is the formulation used in [1], the one in compressibleInterFoam? 2º Is it the same formulation on all branches of OpenFOAM (ESI, ORG and extend)? 3º is dtdg = right and side of the above equation? 4º What is the purpose of doing the dot product (&) between a scalarMatrix and a volScalarField? What is the mathematical representation of this operation? 5º In OpenFOAM(ESI) the compressible part (non-transonic) of the pressure equation we have: Code:
p_rghEqnComp1 =
pos(alpha1)
*(
(
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
+ (alpha1*psi1/rho1)*correction(fvm::ddt(p_rgh))
);
Code:
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
 ? ?6º Apart from [1] is there any other literature on the formulation of compressibleInterFoam? Best Regards! ---- [1] -Miller, S. T., Jasak, H., Boger, D. A., Paterson, E. G., & Nedungadi, A. (2013). A pressure-based, compressible, two-phase flowa finite volume method for underwater explosions. Computers and Fluids, 87, 132–143. https://doi.org/10.1016/j.compfluid.2013.04.002 |
|
|
|

|
|
|
|
|
#69 |
|
Member
hari charan
Join Date: Sep 2021
Location: India,hyderabad
Posts: 97
Rep Power: 5  |
Hi Nat,
I know the post is old. But can you describe the evolution of step 4 mathematically instead of describing it in words? Thanks in advance. |
|
|
|

|
|
|
|
|
#70 |
|
Member
hari charan
Join Date: Sep 2021
Location: India,hyderabad
Posts: 97
Rep Power: 5  |
Hello nat,
Can u explain the evolution of step 3 to step 4 using math instead of words. Thanks in advance. |
|
|
|

|
|
|
|
|
#71 |
|
New Member
Corbin G
Join Date: Oct 2022
Location: Midwest, USA
Posts: 11
Rep Power: 4  |
Dear FOAMers,
Thank you for all the previous contributions to this thread which have helped in my understanding of the compressibleInterFoam solver. Like several others, I am adding some inter-phase mass transfer which requires me to modify the pEqn.H and alphaEqn.H (or perhaps alphaSuSp.H). Therefore, I need a thorough understanding of their structure. I would like to document my findings here to further this thread for future FOAMers, then ask for some of your advices in areas where I am still confused. Part 1 - interFoam I would first like to suggest two excellent resources for understanding the PISO loop in the interFoam (incompressible two-phase volume of fluid) solver. Deshpande et al. derive all the equations in detail, including for the PISO pressure corrector steps: [A] Deshpande, Suraj S., Lakshman Anumolu, and Mario F. Trujillo. "Evaluating the performance of the two-phase flow solver interFoam." Computational science & discovery 5, no. 1 (2012): 014016. http://dx.doi.org/10.1088/1749-4699/5/1/014016 Next, Damian gives a line-by-line commentary of how these are implemented in the interFoam solver, including line-by-line analysis of pEqn.H. I found this very useful: [B] Damian, S. Márquez. "Description and utilization of interFoam multiphase solver." International Center for Computational Methods in Engineering (2012): 1-64. http://www.cfdyna.com/Home/OpenFOAM/...escription.pdf Part 2 - compressibleInterFoam introduction I guess there are three main forks of OpenFOAM which all differ slightly. The source code for the compressibleInterFoam solver for each of these versions can be found: foundation OpenFOAM-10: https://github.com/OpenFOAM/OpenFOAM...sibleInterFoam ESI v2206: https://develop.openfoam.com/Develop...sibleInterFoam foam-extended-5.0: https://sourceforge.net/p/foam-exten...ibleInterFoam/ The foam-extended version has the best documentation in the literature and I will focus on that in this post. It is isothermal (i.e. there is no TEqn.H) and therefore differs substantially from the other versions. The ESI and foundation versions are are very similar. Both solve for temperature in TEqn.H. The foundation version seems to include some built-in functionality for inter-phase mass transfer through the fvModels options. However, the pEqn.H of these two versions is not clear to me. I plan to ask for some advices on these in a later post. Part 3A - compressibleInterFoam foam-extended-5.0 references There are several publications which are closely related to the foam-extended version and can fairly straightforwardly be seen in the pEqn.H. H. Jasak is a co-author on [1] which explains why it more clearly explains the foam-extended version. These include: [1] Miller, S. T., Hrvoje Jasak, D. A. Boger, E. G. Paterson, and A. Nedungadi. "A pressure-based, compressible, two-phase flow finite volume method for underwater explosions." Computers & Fluids 87 (2013): 132-143. http://dx.doi.org/10.1016/j.compfluid.2013.04.002 [2] Koch, Max, Christiane Lechner, Fabian Reuter, Karsten Köhler, Robert Mettin, and Werner Lauterborn. "Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM." Computers & Fluids 126 (2016): 71-90. http://dx.doi.org/10.1016/j.compfluid.2015.11.008 [3] Max Koch Master thesis: Numerical modelling of cavitation bubbles with the Finite Volume method, 2014. https://www.researchgate.net/publica..._Volume_method Of these, [1] and [2] lay out all the essential equations while [3] provides a more detailed discussion of how they are implemented in the foam-extended code. OK, let's go to the equations and code. Part 3B - compressibleInterFoam foam-extended-5.0 pressure equation The basic form of the pressure equation in Miller et al. [1] Equation 15 and Koch et al. [2] Equation 22 is: 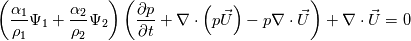 Eq 1 Eq 1Recall:  , based on definition of material derivative and some vector identities , based on definition of material derivative and some vector identitiesNow, looking into the foam-extended pEqn.H, pEqnComp is defined below which is the second term in parenthesis in Eq 1, basically  . .Code:
pEqnComp =
(fvm::ddt(p) + fvc::div(phi, p) - fvc::Sp(fvc::div(phi), p));
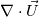 from Eq 1. (See one of the aforemetnioned 2012 publications [A] or [B] on how this the incompressible pressure equation is derived from substituting in a momentum expression into the incompressible continuity equation) from Eq 1. (See one of the aforemetnioned 2012 publications [A] or [B] on how this the incompressible pressure equation is derived from substituting in a momentum expression into the incompressible continuity equation)Code:
fvScalarMatrix pEqnIncomp
(
fvc::div(phi)
- fvm::laplacian(rUAf, p)
);
Code:
solve
(
(
max(alpha1, scalar(0))*(psi1/rho1)
+ max(alpha2, scalar(0))*(psi2/rho2)
)
*pEqnComp()
+ pEqnIncomp
);
Part 3C - compressibleInterFoam foam-extended-5.0 volume of fluid equation Let's move on to the volume of fluid (VoF) equation. The basic form of the pressure equation in Miller et al. [1] Equation 24-25 and Koch et al. [2] Equation 18 is:  Eq 2 Eq 2Now, later on in the pEqn.H we find dgdt: Code:
dgdt =
(pos(alpha2)*(psi2/rho2) - pos(alpha1)*(psi1/rho1))
*(pEqnComp & p);
 Next, in the alphaEqns.H the VoF solution is completed. Recall that (see Eq 3.15 in [3]) OpenFOAM linearizes the source terms and breaks them into two parts like S = Su + Sp*x, where x is the field being solved for. We see in in the alphaEqns.H that Sp is initialized as 0 and Su is initialized as 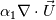 . The Su and Sp are then updated based on dgdt value: . The Su and Sp are then updated based on dgdt value:Code:
forAll(dgdt, celli)
{
if (dgdt[celli] > 0.0 && alpha1[celli] > 0.0)
{
Sp[celli] -= dgdt[celli]*alpha1[celli];
Su[celli] += dgdt[celli]*alpha1[celli];
}
else if (dgdt[celli] < 0.0 && alpha1[celli] < 1.0)
{
Sp[celli] += dgdt[celli]*(1.0 - alpha1[celli]);
}
}
 Plugging in the previously defined dgdt gives: 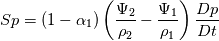 Let's now plug that into the source term equation S = Su + Sp*alpha1 and recall that alpha2 = 1 - alpha1 and we see the complete source term is: 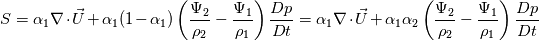 BOOM! It's the complete RHS of the VoF equation Eq 2 from Miller et al. [1] and Koch et al. [2]. Then, the VoF equation is finally solved by passing the RHS source term to the MULES::explicitSolve which I trust considers the LHS of the VoF equation: Code:
MULES::explicitSolve(geometricOneField(), alpha1, phi, phiAlpha1, Sp, Su, 1, 0); Conclusion There you have it folks. I am confident that the foam-extended-5.0 compressibleInterFoam basically solves the pressure equation and the VoF equation described by Miller et al. [1] and Koch et al. [2]. I will discuss the foundation OpenFOAM-10 and ESI v2206 in a future post where I hope you all can help me figure out the formulation. PS1: please point out any mistakes you see and I will try to correct them PS2: keep FOAMing! EDIT: the pressure-velocity coupling and PISO are well-explained in the CFD Direct book Chapter 5: https://doc.cfd.direct/notes/cfd-gen...ocity-coupling Last edited by CorbinMG; January 12, 2023 at 09:44. Reason: add reference to CFD Direct book |
|
|
|

|
|
|
|
|
#72 |
|
New Member
Corbin G
Join Date: Oct 2022
Location: Midwest, USA
Posts: 11
Rep Power: 4  |
EDIT: My analysis is probably not correct in this post because I think I have misinterpreted the correction() function. Please provide your insights into the correction function here: Foam::correction() function
Dear FOAMers, I will continue my previous post, this time looking into the pEqn.H from the ESI and foundation versions, which looks quite a bit different than the foam-extended I discussed previously. I will make use of the same references. The relevant files are: ESI pEqn.H ESI alphaSuSp.H foundation pEqn.H foundation alphaSuSp.H The foundation and ESI versions are quite similar. As of now (ESI might be updated in the future), the main difference is that foundation version has more source term functionality through the "fvModels.source" options. Maybe inter-phase mass transfer can already be accomplished with these options in the foundation version. I will copy the code from the ESI version throughout this post. In pEqn.H (for transonic = no) we find a compressible pressure equation for each phase. Code:
p_rghEqnComp1 =
pos(alpha1)
*(
(
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
+ (alpha1*psi1/rho1)*correction(fvm::ddt(p_rgh))
);
p_rghEqnComp2 =
pos(alpha2)
*(
(
fvc::ddt(alpha2, rho2) + fvc::div(alphaPhi2*rho2f)
- (fvOptions(alpha2, mixture.thermo2().rho())&rho2)
)/rho2
- fvc::ddt(alpha2) - fvc::div(alphaPhi2)
+ (alpha2*psi2/rho2)*correction(fvm::ddt(p_rgh))
);
p_rghEqnComp1  Back in the "if (pimple.transonic())" portion of pEqn.H you will find the below code where the pressure term (the stuff inside the "correction()" command) is expanded to include the divergence terms. I guess if the user chooses "transonic no" the solver assumes the velocity is fairly low and the fvm::ddt(p_rgh) dominates the material derivative of pressure (see my previous post for expansion of Dp/Dt term). I guess in the "transonic no" selection we are assuming  . .Code:
p_rghEqnComp1 =
pos(alpha1)
*(
(
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
+ (alpha1/rho1)
*correction
(
psi1*fvm::ddt(p_rgh)
+ fvm::div(phid1, p_rgh) - fvm::Sp(fvc::div(phid1), p_rgh)
)
);
Next, pEqn.H defines the incompressible portion of the pressure equation as below. This is the same (less the p versus p_rgh difference) across all three version of OpenFOAM. You can checkout the Damian [B] Eq 73, Eq 76, Eq 100, and Eq 124 from my last post to understand this one. I will stick with saying this represents the  part of the pressure equation. part of the pressure equation.Code:
fvScalarMatrix p_rghEqnIncomp
(
fvc::div(phiHbyA)
- fvm::laplacian(rAUf, p_rgh)
);
Code:
solve
(
p_rghEqnComp1() + p_rghEqnComp2() + p_rghEqnIncomp,
mesh.solver(p_rgh.select(pimple.finalInnerIter()))
);
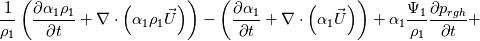 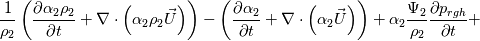 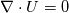 The first term in parenthesis for p_rghEqnComp1 and p_rghEqnComp2 is just the phase mass balance equation, which should be = 0 (see refs [1] and [2]). Maybe it is included just to allow fvOption functionality for boiling, condensation, etc. when phase mass balance  0. In any case, I will assume both those terms equal 0. The second term in parenthesis is the phase mass balance for incompressible (i.e. constant density) flow, like used in the interFoam solver. I am not sure why these are included. However, assuming the phase mass balance terms go to 0 simplifies the pressure equation being solved to: 0. In any case, I will assume both those terms equal 0. The second term in parenthesis is the phase mass balance for incompressible (i.e. constant density) flow, like used in the interFoam solver. I am not sure why these are included. However, assuming the phase mass balance terms go to 0 simplifies the pressure equation being solved to: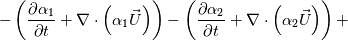  There you have it. Less the incompressible phase mass balance terms, the pressure equation in ESI and foundation version basically looks like Miller et al. [1] and Koch et al. [2] (see Eq 1 in my previous post). Comments on the purpose of including the below in the pressure equation are welcome.  Towards the end of the pEqn.H, dgdt is again defined very similarly to my previous post. Then, the volume of fluid equation is setup in alphaSuSp.H and alphaEqn.H. I won't repeat the analysis here. Note: Be aware that  Best regards, Corbin Last edited by CorbinMG; January 18, 2023 at 16:19. Reason: I am probably wrong... |
|
|
|

|
|
|
|
|
#73 |
|
New Member
Dennis Thuy
Join Date: Apr 2022
Posts: 11
Rep Power: 4  |
Hi Corbin,
Thank you for your elaborate analysis of the pressure equation! I agree with your interpretation of the equation from the ESI version. Unfortunately, I am also not able to explain what exactly the "correction()" function does. I want to comment specifically on the two terms in the pressure equation that represent the phase mass balance for incompressible flow:  Since 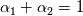 , we can write: , we can write: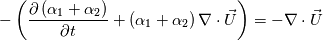 As compressible phase mass balance terms should be equal to zero, this additionally reduces the pressure equation to:  This formulation is significantly different from the formulation in the paper by Miller, as it no longer includes the divergence of the velocity field. Furthermore, as the terms between parenthesis are not equal to zero, except for the incompressible case, this implies that 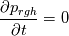 . This is clearly not the desired behavior, and also is not seen in simulation results, where p_rgh does change over time. . This is clearly not the desired behavior, and also is not seen in simulation results, where p_rgh does change over time.Am I making a mistake in rewriting the terms above, or is my observation correct? And if it is correct, what reason do we have to introduce these terms into the pressure equation? Apart from raising additional questions, I would also like to point out that the pressure equation in the ESI version does show the expected behavior in the incompressible limit (i.e. 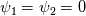 and and 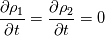 ). In that case, it reduces to the incompressible contribution, ). In that case, it reduces to the incompressible contribution,  . This, however, would also be the case if the incompressible phase mass balance terms were not included in the pressure equation. . This, however, would also be the case if the incompressible phase mass balance terms were not included in the pressure equation.If you have gained any additional insight in the formulation of the pressure equation in the ESI version since your last post, I would be very grateful if you could share this! Kind regards, Dennis |
|
|
|

|
|
 |
| Tags |
| compressible, compressibleinterfoam, theory |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Low Reynolds Number k-epsilon formulation CFX 10.0 | Chris | CFX | 4 | December 8, 2009 00:51 |
| Immersed Boundary Formulation | Rave | Main CFD Forum | 0 | August 11, 2008 15:55 |
| DPM Steady formulation with collisions | kulwinder | FLUENT | 0 | May 22, 2004 19:44 |
| energy equation formulation | Pedro | Phoenics | 1 | July 5, 2001 13:17 |
| Compressible vs. Incompressible formulations | Fernando Velasco Hurtado | Main CFD Forum | 3 | January 7, 2000 17:51 |