 |
|
|
[Sponsors] | |||||
|
|
|
#41 | |
|
New Member
NaiXian Leslie Lu
Join Date: Jun 2009
Location: France
Posts: 26
Rep Power: 17  |
Quote:
Have a good day. Leslie
__________________
Cheers, Leslie LU |
||
|
|

|
||
|
|
|
#42 | |
|
New Member
Cong Gu
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Quote:
dgdt = (psi2 / rho2 - psi1 / rho1) *DDt(p - rho * g * h). But in the derivation, it is dgdt = (psi2 / rho2 - psi1 / rho1) * DDt(p). They are not equivalent, are they? |
||
|
|

|
||
|
|
|
#43 |
|
Member
Richard Kenny
Join Date: Mar 2009
Posts: 64
Rep Power: 18  |
Hello Gucong,
the expression looks like a variation on the original (circa OF17) but I think the same reasoning/derivation still applies, but now of course it appears the 'dynamic' and 'static' components of the pressure are clearly indicated. Recalling that the static contribution is written as p0 + rho (g . z), and hence the sign. I've just scanned the OF23x version of compressibleInterfoam and it seems a lot more is going on in pEqn these days, possibly with a view to stabilizing the explicit terms. If the latter fails then and the average density is varying considerably I think an alternative approach similar to the old dieselFoam might be more appropriate. But that's getting off-topic. Regards, Richard K. |
|
|
|

|
|
|
|
|
#44 | |
|
New Member
Cong Gu
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Quote:
Regards, |
||
|
|

|
||
|
|
|
#45 |
|
Member
Richard Kenny
Join Date: Mar 2009
Posts: 64
Rep Power: 18  |
In p(tot) = pd + p0 + rho (g . z),
p0 = 0 and 'vector' g = (0, 0, -g), which accounts for the sign. Rgds, Richard K. |
|
|
|

|
|
|
|
|
#46 |
|
New Member
Cong Gu
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
||
|
|

|
|
|
|
|
#47 |
|
Member
Richard Kenny
Join Date: Mar 2009
Posts: 64
Rep Power: 18  |
Oh right, sorry for the misinterpretation.
But otherwise, DDt(p) != DDt(p_rgh) owing to the spatial cpt of DDt(..), but presumably this latter is assumed to be much smaller than the value of ddt(p). It would be interesting to verify numerically. RGK |
|
|
|

|
|
|
|
|
#48 |
|
Member
james wilson
Join Date: Aug 2014
Location: Orlando, Fl
Posts: 39
Rep Power: 12  |
Kenny,
Thanks for your guidance on this topic. Your reference to: fvScalarMatrix psiConvectionDiffusion ( fvm::ddt(rho, psi) + fv::gaussConvectionScheme<scalar>(mesh, phi, UDs).fvmDiv(phi, psi) //- fv::gaussLaplacianScheme<scalar, scalar>(mesh, CDs, snGrads) //.fvmLaplacian(Dpsif, psi) - fvm::Sp(Sp, psi) - Su ); Is found in "IMULESTemplates.C" for a call to Foam::MULES::implicitSolve. We however are using a call to Foam::MULES::explicitSolve found in MULESTemplates.C (as youve specified) where the structure of the fvScalarMatrix is less clear: " template<class RhoType, class SpType, class SuType> void Foam::MULES::explicitSolve ( const RhoType& rho, volScalarField& psi, const surfaceScalarField& phi, surfaceScalarField& phiPsi, const SpType& Sp, const SuType& Su, const scalar psiMax, const scalar psiMin ) { const fvMesh& mesh = psi.mesh(); const scalar rDeltaT = 1.0/mesh.time().deltaTValue(); psi.correctBoundaryConditions(); limit(rDeltaT, rho, psi, phi, phiPsi, Sp, Su, psiMax, psiMin, 3, false); explicitSolve(rDeltaT, rho, psi, phiPsi, Sp, Su); } " Could you comment on this portion of the code and extend your explanation to cover this specific template the compressibleInterFoam solver uses? Your explanation of the source term implementation using "fvScalarMatrix psiConvectionDiffusion (...)" makes sense but THIS template is not being used. I am assuming MULES::explicitSolve operates the same way as MULES::implicitSolve in terms of how the source terms are passed using the template where the solution of course is different. Using this style of source term distribution in openFoam, I have been able to validate analytic Stefan type problems, so I do not doubt it's validity one bit. I would however, like to gain a deeper understanding of the form of the FV equations such that I can get creative with new source terms. I've modified the compressibleInterFoam solver to output Su, Sp and divU (=alpha1*divU). I have a line plot along the center-line at y and a surface plot of Su and Sp at the instant the line plots are shown in the attached images. I hope this helps with visualization. Looking at the surface plot of Sp, there are portions of the gaseous phase where Sp is non zero. I would assume that this non zero contribution in the alpha equation would lead to un-bounding of alpha in the gasseous phase. If the solver does take the form described by kenny where Sp --> Sp*alpha1 however, this non zero portion would have no contribution since alpha = 0 in this region and therefore would support Kenny's argument. One final note, The images shown here correspond to expanding gas.. when the gas cools due to convection and diffusion of thermal energy, the sign of the source terms change since the gas is now contracting and the interface must move inward, and as a result, the assignment of divU should change as well divU --> Su (expand) vs. divU --> Sp (contract) to promote diagonal dominance. It is not treated intuitively in this manner in the default solver. Food for thought ; ) James Su: Screenshot from 2014-12-12 08:59:22.jpg; Sp: Screenshot from 2014-12-12 09:03:51.jpg Last edited by jameswilson620; December 12, 2014 at 10:17. Reason: adding result data |
|
|
|

|
|
|
|
|
#49 | |
|
Senior Member
Dongyue Li
Join Date: Jun 2012
Location: Beijing, China
Posts: 848
Rep Power: 18  |
Quote:
DDt( rho1 ) = DDt( rho1_0 ) + (psi1 / rho1) DDt( p )  If Im wrong correct it pls. |
||
|
|

|
||
|
|
|
#50 |
|
Member
james wilson
Join Date: Aug 2014
Location: Orlando, Fl
Posts: 39
Rep Power: 12  |
So in case anyone is interested..
a call to MULES::explicitSolve(geometricOneField(), alpha1, phi, tphiAlpha(),Sp,Su, 1, 0); references this template in MULESTemplates.C for OF2.3 Code:
template<class RhoType, class SpType, class SuType>
void Foam::MULES::explicitSolve
(
const RhoType& rho,
volScalarField& psi, // Note the use of the pointer, I believe this is how psi is updated without explicitly defining a "return psi"
const surfaceScalarField& phi,
surfaceScalarField& phiPsi,
const SpType& Sp,
const SuType& Su,
const scalar psiMax,
const scalar psiMin
)
{
const fvMesh& mesh = psi.mesh();
const scalar rDeltaT = 1.0/mesh.time().deltaTValue();
psi.correctBoundaryConditions();
limit(rDeltaT, rho, psi, phi, phiPsi, Sp, Su, psiMax, psiMin, 3, false); //I haven't looked much into this
explicitSolve(rDeltaT, rho, psi, phiPsi, Sp, Su); //CALL TO ANOTHER TEMPLATE WHERE PSI IS SOLVED FOR THE NEXT TIME STEP
}
Code:
template<class RdeltaTType, class RhoType, class SpType, class SuType>
void Foam::MULES::explicitSolve
(
const RdeltaTType& rDeltaT,
const RhoType& rho,
volScalarField& psi,
const surfaceScalarField& phiPsi,
const SpType& Sp,
const SuType& Su
)
{
Info<< "MULES: Solving for " << psi.name() << endl;
const fvMesh& mesh = psi.mesh();
scalarField& psiIf = psi; // initialize psiIf
const scalarField& psi0 = psi.oldTime(); // Store old values of psi for solution
psiIf = 0.0; // Set psiIf to zero
fvc::surfaceIntegrate(psiIf, phiPsi); // Calculate divergence of phiPsi; update psiIf as result
//NOTE: psiIf is utilized for two purposes here. It is used to advance psi in time (what were after) and also as a temporary dummy variable to store the value of the divergence of phiPsi
if (mesh.moving())
{
psiIf =
(
mesh.Vsc0()().field()*rho.oldTime().field()
*psi0*rDeltaT/mesh.Vsc()().field()
+ Su.field()
- psiIf
)/(rho.field()*rDeltaT - Sp.field());
}
else
{
// VOF EQUATION
// (psiIf(unknown) - psi0)/dt + psiIf(known dummy place holder for divergence of phiPsi) = psiIf(unknown)*Sp + Su
// OR
// ddt(psi) + div(phiPsi) = psi*Sp + Su
// Now solve for psiIf, the unknown value of psiIf at t+dt by re arranging the above expression
psiIf =
(
rho.oldTime().field()*psi0*rDeltaT
+ Su.field()
- psiIf // Divergence
)/(rho.field()*rDeltaT - Sp.field());
}//NOTE rho.field() is geometricOneField() (simply = 1)
psi.correctBoundaryConditions();
}
Can anyone comment on limit(rDeltaT, rho, psi, phi, phiPsi, Sp, Su, psiMax, psiMin, 3, false) from the first template? James |
|
|
|

|
|
|
|
|
#51 |
|
New Member
Sasa Goran
Join Date: Feb 2015
Location: Japan
Posts: 23
Rep Power: 11  |
OK, i've been looking at this transportationProperties file for a couple of days now, and i'm none the wiser. I guess i figured out how to set rho0 (initial density, i guess, and equals 0 for compressible fluids) and pMin (i guess it's the minimum pressure, and should be above 0) but this psi thing bother me to death. It's compresibity, but i've never seen such a formulation, all the data i can get for psi is for the [1/MPa] unit, not the [s^2/m^2] as specified in the file.
I would grealty appreciate it if someone could help me out in finding the values for psi (ATM i need water and air) or tell me where a good database is. Also culd you clarify my guesses about rho0 and pMin, or explain what they are indeed. Thank you guys in advance. Edit: OK found out. The 1/MPa formulation comes from \beta = ( d_rho / d_p ) / rho So multiplying beta by rho should give psi Last edited by Supersale; March 31, 2015 at 02:03. |
|
|
|

|
|
|
|
|
#52 | |
|
New Member
|
Quote:
I saw three expressions for rho: rho1 = rho1_0 + psi1 * p rho1 = rho1_0 + psi1 * (p - p_0) rho1 = psi1 * p In all cases, rho1_0 and p_0 are constants, their material derivative should be zero. From its definition, psi1 is isothermal compressibility, aka, be a constant when temperature fixed. So, DDt(rho1) = psi1 * DDt(p) |
||
|
|

|
||
|
|
|
#53 | |
|
New Member
|
Hi guys,
Recently I'm learning the solver compressibleInterFoam in OpenFOAM-2.3.x. From the discussion above, I've already figure out the pressure equation and alpha equation, What bothers me is the temperature equation, which seems to be derived from specific total internal energy equation: ddt(rho * e) + div(rho * U * e) + ddt(rho * K) + div(rho * U * K) = -div(U * p) + laplacian((Cp/Cv) * (kappa / Cp), e) where e = Cv * T, e has dimension J/kg, and Cv has dimension J/kg/K. For a multiphase flow, and in solver's description: Quote:
But for specific total internal energy, the equation is derived based on the conservation of energy in a control volume (cell). I think the total energy in a computation cell should be taken as mass average of both phases. Let us use Y1, Y2 denote mass fraction and alpha1, alpha2 denote the volume fraction of two phases. And Cv denotes the specific heat capacity at constant volume of the mixture, Cv1 and Cv2 for each phase. In my opinion, Cv = Y1*Cv1 + Y2*Cv2, so let the energy equation be devided by Cv, we get ddt(rho * T) + div(rho * U * T) - laplacian((Cp/Cv) * (kappa / Cp), T) + (ddt(rho * K) + div(rho * U * K) + div(U * p))/Cv = 0 but in the TEqn: Code:
fvScalarMatrix TEqn
(
fvm::ddt(rho, T)
+ fvm::div(rhoPhi, T)
- fvm::laplacian(twoPhaseProperties.alphaEff(turbulence->mut()), T)
+ (
fvc::div(fvc::absolute(phi, U), p)
+ fvc::ddt(rho, K) + fvc::div(rhoPhi, K)
)
*(
alpha1/twoPhaseProperties.thermo1().Cv()
+ alpha2/twoPhaseProperties.thermo2().Cv()
)
);
Also I think the term twoPhaseProperties.alphaEff(turbulence->mut()) should be twoPhaseProperties.alphaEff(turbulence->alphat()) or turbulence->alphaEff(), note that the last two expression are equivalent. The only difference is that in OpenFOAM alphat = mut / Prt. Can anybody help me with these? |
||
|
|

|
||
|
|
|
#54 | |
|
New Member
Cong Gu
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Quote:
http://www.sciencedirect.com/science...45793013001229 |
||
|
|

|
||
|
|
|
#55 | |
|
New Member
Cong Gu
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Quote:
ddt( alpha_1 * rho_1 * (Cv_1 * T + K) ) + div( alpha_1 * rho_1 * U * (Cv_1 * T + K) ) - laplacian(kappa_1 , T ) * alpha_1 * rho_1 / rho + div( p * U ) * alpha_1 * rho_1 / rho + alpha_1 * rho_1 * g dot U = 0 Note that the thermal diffusion and mechanical work are distributed to the phases in proportion to the mass. Then expand the first two terms by product rule and apply conservation of phase mass ddt(alpha_1 * rho1) + div(alpha_1 * rho_1 * U) = 0 Should get alpha_1 * rho_1 * ddt(Cv_1 * T + K) + alpha_1 * rho_1 * U dot grad(Cv_1 * T + K) for the first two terms. And let alpha_Eff = (alpha_1 * kappa_1 / Cv_1) + (alpha_2 * kappa_2 / Cv_2) Divide the whole equation by (rho_1 * Cv_1), maybe assuming constant Cv_1. Then sum it with the similar equation for phase 2. Finaly multiply the sum with rho. You should arrive at similar things in the code, except some small deviations in the work of gravity. They use p_rgh instead of p, which should take care of work by gravity. But it gets complicated if rho is changing. Last edited by gucong; October 11, 2015 at 05:33. |
||
|
|

|
||
|
|
|
#56 | |
|
New Member
|
Quote:
It's more clear now. But I don't understand the div( p * U ) * alpha_1 * rho_1 / rho term, should it be div( p * U ) * alpha_1? |
||
|
|

|
||
|
|
|
#57 |
|
New Member
Jan Behrendt
Join Date: Nov 2016
Location: Germany
Posts: 3
Rep Power: 10  |
Hi Foamers,
thanks for the benefical discussion above. Recently i'm also trying to figure out the compressibleInterFoam Solver (Version 2.3.x) in addition, i'm pretty new to OF, so please be kind  I already figured out the alphaEqn (including the correct use of MULES) but im struggling with the pEqn. To be more exact I didn't get that pEqnComp part. I guess piprus attached file could help me a lot, but unfortunately it's not available any more  . .may someone can help me understanding the correct derivation of the pEqn or can give me a hint how the main equation looks like? maybe it's an easy, or even a silly, question but i didn't get that part and in my opinion there is a lack of compressible multiphase flow literature especially for compressibleInterFoam. Hence, i need some help  Thanks in advance 
|
|
|
|

|
|
|
|
|
#58 | |
|
New Member
Jan Behrendt
Join Date: Nov 2016
Location: Germany
Posts: 3
Rep Power: 10  |
Hey gucong,
i got a question about that derivation you've posted here: Quote:
i tried to follow your derivation but i guess i've made a mistakesomewhere. After dividing the whole eqn by (rho_1*Cv_1) we should get: alpha_1*ddt(T)+alpha1*U dot grad(T) + alpha1/Cv_1*ddt(K) + alpha1/Cv_1*U dot grad(K) + div(p*U)*alpha1/Cv_1/rho - laplacian(kappa_1, T)*alpha1/Cv_1/rho summing it with the similar eqn for phase 2 and multiply the sum with rho we should get: rho*ddt(T) + rho*U dot(T) - laplacian(alphaEff , T) ... (+ rate of changes due to mechanical, or kinetic, energy) the code tells us that the time derivation term should be ddt(rho, T) may you can tell me where i did a mistake? |
||
|
|

|
||
|
|
|
#59 |
|
New Member
Daniel Duque
Join Date: Oct 2018
Posts: 3
Rep Power: 8  |
Hello, everyone.
First, thanks to all that have contributed to this thread, which has really helped me understand this solver. Specially, references to the article by Miller, Jasak, Boger, Paterson and Nedungadi (C&F 87, 2013). If I understand correctly, we have equations like: (1) 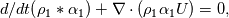 which may be written as (2) ![\rho_1 [ d/dt (\alpha_1) + \nabla\cdot ( \alpha_1 U ) ] + \alpha_1 D/Dt(\rho_1) = 0, \rho_1 [ d/dt (\alpha_1) + \nabla\cdot ( \alpha_1 U ) ] + \alpha_1 D/Dt(\rho_1) = 0,](/Forums/vbLatex/img/c98893787f532dc2e9536c22679e9d86-1.gif) where DDt is the convective time derivative. But if rho1 is a function of the pressure, then DDt(rho1) = psi1 * DDt(p), where psi1 is the derivative d(rho1)/d p . This means the equation may be written as (3) ![\rho_1 [ d/dt (\alpha_1) + \nabla\cdot ( \alpha_1 U ) ] = - \alpha_1 * \psi_1 / \rho_1 D/Dt(\rho_1) . \rho_1 [ d/dt (\alpha_1) + \nabla\cdot ( \alpha_1 U ) ] = - \alpha_1 * \psi_1 / \rho_1 D/Dt(\rho_1) .](/Forums/vbLatex/img/0e2c15e004c4288aa46721083862a99a-1.gif) Similarly for the other fraction, alpha2. Now, Miller at all start doing combinations with these equations, but on the latest OF 6 code we find this, in pEqn.h Code:
p_rghEqnComp1 =
pos(alpha1)
*(
(
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
+ (alpha1*psi1/rho1)*correction(fvm::ddt(p_rgh))
);
Code:
(
fvc::ddt(alpha1, rho1) + fvc::div(alphaPhi1*rho1f)
- (fvOptions(alpha1, mixture.thermo1().rho())&rho1)
)/rho1
Code:
- fvc::ddt(alpha1) - fvc::div(alphaPhi1)
+ (alpha1*psi1/rho1)*correction(fvm::ddt(p_rgh))
Then, after pressure is solved for, dgdt is computed as : Code:
dgdt =
(
alpha1*(p_rghEqnComp2 & p_rgh)
- alpha2*(p_rghEqnComp1 & p_rgh)
);
(4) 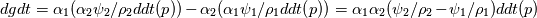 Then, we find on alphaSuSp these two terms, defined if dgdt>0 as: Code:
Sp[celli] -= dgdt[celli]/max(1.0 - alpha1[celli], 1e-4);
Su[celli] += dgdt[celli]/max(1.0 - alpha1[celli], 1e-4);
Code:
fvScalarMatrix alpha1Eqn
(
(
LTS
? fv::localEulerDdtScheme<scalar>(mesh).fvmDdt(alpha1)
: fv::EulerDdtScheme<scalar>(mesh).fvmDdt(alpha1)
)
+ fv::gaussConvectionScheme<scalar>
(
mesh,
phiCN,
upwind<scalar>(mesh, phiCN)
).fvmDiv(phiCN, alpha1)
// - fvm::Sp(fvc::ddt(dimensionedScalar("1", dimless, 1), mesh)
// + fvc::div(phiCN), alpha1)
==
Su + fvm::Sp(Sp + divU, alpha1)
);
So, I guess it all makes sense. I would appreciate comments on this, since in my group we are trying to add a phase-change term to the phase equations, which would read: 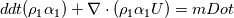 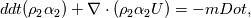 where mDot is a source term. This will modify all these expressions, and I’d like to make sure we get it right. Btw, I do know there is a solver that includes phase change, but that one is incompressible, and the approach is quite different. |
|
|
|

|
|
|
|
|
#60 |
|
New Member
Daniel Duque
Join Date: Jan 2011
Location: ETSIN, Madrid
Posts: 28
Rep Power: 15  |
Just a quick note to this, dduque, is my usual name. I had to use the previous one, ddcampayo, due to some glitch in the CFD-online user management system. BTW, I am quite convinced my interpretation is mostly correct, with some technical details that I had wrong. If anyone is interested I can correct those. |
|
|
|

|
|
 |
| Tags |
| compressible, compressibleinterfoam, theory |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Low Reynolds Number k-epsilon formulation CFX 10.0 | Chris | CFX | 4 | December 8, 2009 00:51 |
| Immersed Boundary Formulation | Rave | Main CFD Forum | 0 | August 11, 2008 15:55 |
| DPM Steady formulation with collisions | kulwinder | FLUENT | 0 | May 22, 2004 19:44 |
| energy equation formulation | Pedro | Phoenics | 1 | July 5, 2001 13:17 |
| Compressible vs. Incompressible formulations | Fernando Velasco Hurtado | Main CFD Forum | 3 | January 7, 2000 17:51 |