 |
|
|
[Sponsors] | |||||
|
|
|
#41 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear Gerald,
thanks for the feedback. I think I get the point. That means if I make a RANS calculation and I am really interested in the real reynolds-averaged pressure (due to the fact that we split the stress tensor into hydrostatic and deviatoric -> shear-rate; as you told), I have to substract p with 2/3*k. I am correct?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#42 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear all,
the latest news about the [math]2/3 k \delta_{ij}[/term]. As Gerhald told, this term could be included into the pressure to get some modified pressure field (Pope). But till now I think this term is neglected in OpenFOAM because:
http://www.cfd-online.com/Forums/ope...-stresses.html http://www.cfd-online.com/Forums/ope...sonicfoam.html http://www.cfd-online.com/Forums/ope...oam-2-2-x.html Therefore I still keep the PDF as it is (if you dont know which PDF I mean): http://www.cfd-online.com/Forums/ope...-openfoam.html Feel free to correct me!
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#43 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear all,
I was wrong with the assumption that the term  is neglected. As Gerhard mentioned before, it is pushed into a modified pressure. For me it was obvious after I derived the equations myself. If you want to check it out, you find the derivations and the analogy of Cauchy-Stress tensor and Reynolds-Stress tensor here: is neglected. As Gerhard mentioned before, it is pushed into a modified pressure. For me it was obvious after I derived the equations myself. If you want to check it out, you find the derivations and the analogy of Cauchy-Stress tensor and Reynolds-Stress tensor here:http://www.cfd-online.com/Forums/ope...-openfoam.html
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#44 |
|
Senior Member
Ehsan
Join Date: Mar 2009
Posts: 112
Rep Power: 17  |
Dear Tobias
There is a GenSGSStress.C (in turbulenceModels/Incompressible/LES), which is called by DeardorffDiffStress model, where the SGS stress tensor (B) is also computed in addition to nuSgs. We went deep into the equations but we were not able to derive the formula in the second line (fvc:laplacian ...) compared to the function divDevReff in GenEddyVisc.C. Would you please help us and say how this line is derived from the momentum equation? Regards fvc::div(B_) + fvc::laplacian(nuSgs_, U, "laplacian(nuEff,U)") - fvm::laplacian(nuEff(), U) |
|
|
|

|
|
|
|
|
#45 | |
|
Senior Member
Ehsan Asgari
Join Date: Apr 2010
Posts: 473
Rep Power: 18  |
Quote:
My understanding is that second line is for stability purposes. Since nuEff is the sum of nuSgs and nuLam, by neglecting fvc and fvm operators one can expect that nuSgs cancels out in second and third lines, yielding a simple laplacian(nuLam,U). Regards |
||
|
|

|
||
|
|
|
#46 |
|
Senior Member
Ehsan
Join Date: Mar 2009
Posts: 112
Rep Power: 17  |
Dear Ehsan
Thank you for your helps and the rational reply. Regards |
|
|
|

|
|
|
|
|
#47 |
|
Senior Member
Ehsan
Join Date: Mar 2009
Posts: 112
Rep Power: 17  |
Hello,
I would be happy if anyone could help for the post in: http://www.cfd-online.com/Forums/ope...dorff-sgs.html Regards |
|
|
|

|
|
|
|
|
#48 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Dear all,
Thank you for the Explanation Tobias. I have been immersed in the Topic with the OpenFOAM4.x that with OpenFOAM3.x Change the Turbulence model Code structure. Before we had dev Operator for incompressible flow and dev2 Operator for compressible flow. For incompressible flow, as you said a "stabilization term" have been add to the laplacian of the velocity,  I don't get the stabilization choice of  but ok, the term would be Zero for incompressible flow (converged as you mentionned). but ok, the term would be Zero for incompressible flow (converged as you mentionned).Now, all the code have the dev2 Operator, Thanks to this the compressible and incompressible turbulence model have a common Framework  And now, we have the "stabilization term" for incompressible that is  Why not! But the question I have now : how can the stabilization term can be choose for incompressible flow, it is convenient to be 1/3 but before that was 2/3, so what is the meaning difference in the Resolution? |
|
|
|

|
|
|
|
|
#49 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
your last equations are not correct. It should be two thirds. In general we could just remove the term (at least for incompressible) fluids but why should we? The continuity is not zero based on the iteration procedure (as you already states) and it is a good choice o track the error. Why they use 2/3 for now, might come from numerical analyzes or from code style / structure base as you already said - Framework is similar. But don't ask me about that real intension. However, we could also add  but of course we would somehow amplify the error term. I think the limit would be one (naturally) and above one would make no sense. Going to one might be also not the best choice. However, using dev2 everywhere makes the code style more equal but again, do not ask me why they introduced dev to be dev2 for incompressible solvers. From a mathematical point of view there is nothing to say against this implementation. but of course we would somehow amplify the error term. I think the limit would be one (naturally) and above one would make no sense. Going to one might be also not the best choice. However, using dev2 everywhere makes the code style more equal but again, do not ask me why they introduced dev to be dev2 for incompressible solvers. From a mathematical point of view there is nothing to say against this implementation.PS: Using two thirds instead of one third should accelerate the solution convergence.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#50 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
I think, the last equation is correct but I didn't explain the Background correctly.
My simple calculation is for the stress Tensor, with stokes hypothesis:  with  and and  and and   we retrieve the compressible Navier Stoke equation. Recalling     For incompressible and compressible flow formulation in OF3.x and OF4.x.  The dev2 use 2/3 factor but it is to lead to 1/3 factor in the stress Tensor for the part with the  Before,  with  So  As I said, the previous implementation for incompressible flow we had  But the  in converged flow, so as you said it would be a stabilization term in converged flow, so as you said it would be a stabilization termand for compressible flow as expected for Navier stoke equation for compressible  Now Incompressible and compressible flow have been write to use dev2 in the turbulence model so  But we don't get how is impacted the stability/accurancy by the formulation for incompressible with 1/3 instead of the previous 2/3 By the way, don't be worry if your old case file with the new OpenFOAM3.x and OpenFOAM4.x says Code:
keyword div((nuEff*dev2(T(grad(U))))) is undefined in dictionary |
|
|
|

|
|
|
|
|
#51 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
I will check your stuff but did you ever checked out my derivation of my book? Out of the box I would not agree with you because in my book I did it for 2.3.x and for incompressible we got the shear-rate tensor to be:
 and for compressible we got:  I also checked the 4.x and there I got the incompressible one to be like the compressible. However, one thing. You made effort to your equations, however, for reading it, operators should not be italic and you should also use bold symbols (maybe it is just my opinion but it would be much better in reading). However, if you are talking for compressible stuff you should use the dynamic visco instead of the kinematic one. Of course it is obvious but however, it is not correct. PS: That the keyword is not defined or missing is clear if you understand the structure change in FOAM (not a big deal).
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#52 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Hi,
Sorry for the bold, I spent a couple of hours to get the tricks so I wanted to share. It seems to me that you mistake between dev or dev2 and the stress tensor. I didn't read your book but I read carrefully the derivation on your threads. I was not convinced by it. In a simple way starting from the definition of the stress tensor for newtonian with Stoke hypothesis, for me it is clear know for the OF2.x and for the later ones. My mistake to use kinematic viscosity. I was focus into dev and dev2 operator for the stress tensor, to retrieve the common Navier-Stokes. Sorry. The change of the structure would not be a big deal for you, cool. For me, it is Always good to understand why the keyword have changed and what is the equations solved. I get the impression that you think you are the best who know every thing and that you mock me. Not a problem. Lucky you. I am happy to found the answer to my question, and I find the proof without Black box, that is clear and coherent with the common equation. I hope at least that could help someone which was the aim of publishing. Not to be despise. Tchuss! |
|
|
|

|
|
|
|
|
#53 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Hi,
Sorry for the bold, I spent a couple of hours to get the tricks so I wanted to share. It seems to me that you mistake between dev or dev2 and the stress tensor. I didn't read your book but I read carrefully the derivation on your threads. I was not convinced by it. In a simple way starting from the definition of the stress tensor for newtonian with Stoke hypothesis, for me it is clear know for the OF2.x and for the later ones. My mistake to use kinematic viscosity. I was focus into dev and dev2 operator for the stress tensor, to retrieve the common Navier-Stokes. Sorry. The change of the structure would not be a big deal for you, cool. For me, it is Always good to understand why the keyword have change and what is the equations solved. I get the impression that you think you are the best who know every thing and that you mock me. Not a problem. Lucky you. I am happy to found the answer to my question, and I find the proof without Black box, that is clear and coherent with the common equation. I hope at least that could help someone that was the aime of publishing. Not to be despise. Tchuss! |
|
|
|

|
|
|
|
|
#54 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
You are Kind to say that I know everything. As you can see I try to help people, not to convince them by the stuff I did. Finally, I derived the equations myself and I also might did something wrong. As I already said, I will check what you did but however it seems to me that you don't want it. if you think that I think I know everything
 nice - if you would know me better you would know that I really do not know too much. If you feel pissed of by me, I am sorry. I just mentioned that I do not agree to your statement till now but it seems that you derived it, showed yourself that you are right and just insult me without any reason. nice - if you would know me better you would know that I really do not know too much. If you feel pissed of by me, I am sorry. I just mentioned that I do not agree to your statement till now but it seems that you derived it, showed yourself that you are right and just insult me without any reason.You know why I mentioned to make the equations correct? Because in every literature you find different stuff and it is just the lazyness to make things clear. If someone who is not familiar with the mathematical stuff he might be confused because you used kinematic visco instead of dynamic etc. But however, screw me, insult me and blame me ... If there would be more guys like you who put such an effort in the derivatives I would be much happier because I could lern more and the discussions would be better. But as I stated, I will check your stuff - even if I get pissed off of your message -> "You feel like you are the best and know anything"... Wow ... If it would 've so, I would not discuss here and if you even read the whole thread you would see that I already made a lot of mistakes here. Sent from my HTC One mini using CFD Online Forum mobile app
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#55 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Tobi,
It is Bad that now we are stuck in this reproach things. I apologize if I offend you. I get the need to have clear syntaxe for equation. I am totally agree with you. Can we start again, and if you have time have a look to the équation to know if I made a mistake. That would be great to have your check. Have a nice day/evening what ever Time Line you are! |
|
|
|

|
|
|
|
|
#56 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear Emeline,
The stuff I wrote today - similar to yours » I am just a normal guy who tries (maybe like you) to understand all the complex things in FOAM, Numerics etc. and I am just a human who can have a bad day or a more stressful day, like last week Friday, too. However, the only thing that I did not like was the fact that you blamed me (more or less) that I think I am the best and greatest guy here. It was disappointing because finally I do so many things in my spare time without any benefit for the community. I made so many effort to clear things that are not obvious at the first moment and showed it to the community. But I have to say that it is my knowledge based on the literature I read and the derivations I did (and I could be wrong in any case as I was already in this thread - just see the term 2/3 k rho). Honestly, I have to say that I am not an expert and I do not feel like to be one. As I already said I only want to get the fundamentals and understand what is going on (especially in the code and with the equations) - I think like you. Back to the topic. As I stated above, I did not agree with your statement you gave but maybe I got just something wrong, which I did in fact, but I also mentioned that I have to check it before. The problem was just a sign that I did not check when I said your  is wrong (no time for checking on Thursday). However, now I got your point and your derivations are correct. Finally, there is nothing left to say. The only thing is, that I did my derivations differently and the benefit of using dev2 is (maybe) more clearer that it has more impact on the stability. is wrong (no time for checking on Thursday). However, now I got your point and your derivations are correct. Finally, there is nothing left to say. The only thing is, that I did my derivations differently and the benefit of using dev2 is (maybe) more clearer that it has more impact on the stability.The main difference in the derivation is, that you put two terms together. First of all I will talk about my point of view while I take your stuff into account. I will first start with the real fundamentals now. The shear-rate tensor for Newtonian fluids can be expressed based on the following formula [22]:  As you stated, using the Stokes relation (bulk viscosity = 0), it follows that:  and in Newtonian fluids we replace  . This can be checked out in [22], if this literature is not available, I made the same derivation in my book chapter 7 where I showed the ?correct? bulk viscosity term (in each literature you can find different stuff like [16] and [22]) and the Stokes relation and why we end up with the common shear-rate tensor (http://www.holzmann-cfd.de/index.php...s-and-openfoam): . This can be checked out in [22], if this literature is not available, I made the same derivation in my book chapter 7 where I showed the ?correct? bulk viscosity term (in each literature you can find different stuff like [16] and [22]) and the Stokes relation and why we end up with the common shear-rate tensor (http://www.holzmann-cfd.de/index.php...s-and-openfoam):  is the strain-rate tensor as you also already stated to be is the strain-rate tensor as you also already stated to be ![\textbf{D} = \frac{1}{2}\left[\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\text{T}\right] \textbf{D} = \frac{1}{2}\left[\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\text{T}\right]](/Forums/vbLatex/img/b4030f3dab25859d8a3eac1f0523d233-1.gif) . It should be noted that the above fundamental equation is only valid if T is a symmetric tensor and the viscosity of the fluid has to follow a linear law [22]. I think till here everything is clear. Using your mathematical stuff: . It should be noted that the above fundamental equation is only valid if T is a symmetric tensor and the viscosity of the fluid has to follow a linear law [22]. I think till here everything is clear. Using your mathematical stuff: , the above shear-rate tensor can be rewritten to: , the above shear-rate tensor can be rewritten to: Now you added the laplacian operator which is good because we split implicit and explicit part (laplacian can be treated implicit). Doing so, we first have to apply the divergence operator to the shear-rate tensor (I also add the definition of the strain-rate tensor): ![\nabla \bullet \boldsymbol{\tau} = \nabla \bullet \left\{ 2\mu \left(\frac{1}{2} \left[\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\text{T}\right]\right) - \frac{2}{3} \mu (\nabla \bullet \textbf{U})\textbf{I}\right\} \nabla \bullet \boldsymbol{\tau} = \nabla \bullet \left\{ 2\mu \left(\frac{1}{2} \left[\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\text{T}\right]\right) - \frac{2}{3} \mu (\nabla \bullet \textbf{U})\textbf{I}\right\}](/Forums/vbLatex/img/6523598e980c37d68213abc6de9d10ad-1.gif) Now I get similar stuff like you, while extracting the brackets and the divergence operator: ![\nabla \bullet \boldsymbol{\tau} = \nabla \bullet \left[ \mu \left(\nabla \otimes \textbf{U}\right)\right] + \nabla \bullet \left[\mu \left(\nabla \otimes \textbf{U})^\text{T}\right)\right] - \nabla \bullet \left[\frac{2}{3} \mu (\nabla \bullet \textbf{U})\textbf{I} \right] \nabla \bullet \boldsymbol{\tau} = \nabla \bullet \left[ \mu \left(\nabla \otimes \textbf{U}\right)\right] + \nabla \bullet \left[\mu \left(\nabla \otimes \textbf{U})^\text{T}\right)\right] - \nabla \bullet \left[\frac{2}{3} \mu (\nabla \bullet \textbf{U})\textbf{I} \right]](/Forums/vbLatex/img/165f96caf0a00520a4bf429ea75b799d-1.gif) This equation exact the same like yours in line 3, if we assume constant viscosity: ![\nabla \bullet \boldsymbol{\tau} = \mu \Delta \textbf{U} + \mu \nabla \bullet \left(\nabla \otimes \textbf{U}\right)^\text{T}- \mu \nabla \bullet \left[\frac{2}{3} (\nabla \bullet \textbf{U})\textbf{I} \right] \nabla \bullet \boldsymbol{\tau} = \mu \Delta \textbf{U} + \mu \nabla \bullet \left(\nabla \otimes \textbf{U}\right)^\text{T}- \mu \nabla \bullet \left[\frac{2}{3} (\nabla \bullet \textbf{U})\textbf{I} \right]](/Forums/vbLatex/img/5afaedb9b627e0d9cba7dec839f08d13-1.gif) Incompressible in FOAM and DEV To be comform with your equation in line 3, lets assume constant density in addition. So we divide and get the kinematic viscosity. Now, I realized the difference in our derivation. You added the last two terms together (which I will not do). It follows: ![\frac{1}{\rho}\nabla \bullet \boldsymbol{\tau} = \nu \Delta \textbf{U} + \nu \nabla \bullet \left(\nabla \otimes \textbf{U}\right)^\text{T}- \nu \nabla \bullet \left[\frac{2}{3} (\nabla \bullet \textbf{U})\textbf{I} \right] \frac{1}{\rho}\nabla \bullet \boldsymbol{\tau} = \nu \Delta \textbf{U} + \nu \nabla \bullet \left(\nabla \otimes \textbf{U}\right)^\text{T}- \nu \nabla \bullet \left[\frac{2}{3} (\nabla \bullet \textbf{U})\textbf{I} \right]](/Forums/vbLatex/img/c6e172358d768395d464cceb01c2af27-1.gif) For incompressible treatments we have divDevReff which (my interpretation) stands for divergence of the Deviatoric part of the Reynolds-Average approach. And of course we are interested in the effective transport (laminar + turbulent). The call is as follow: divDevReff(U) in the UEqn.H files. (Now I am not sure where we go because I have no debug-version here and could not use gdb). However, a short code exploration lead me to the following. The divDevREff function is implemented in incompressible/IncompressibleTurbulenceModel/IncompressibleTurbulenceModel.C which is redirecting to the function divDevRhoReff(U). Without gdb it is a bit hard now. Well, based on the fluid we are using, we probably would be redirected (for Newtonian fluids) to: linearViscousStress/linearViscousStress.C: where we will find the definition of the divDevRhoReff(U) function. Here we have: Code:
template<class BasicTurbulenceModel>
Foam::tmp<Foam::fvVectorMatrix>
Foam::linearViscousStress<BasicTurbulenceModel>::divDevRhoReff
(
volVectorField& U
) const
{
return
(
- fvc::div((this->alpha_*this->rho_*this->nuEff())*dev2(T(fvc::grad(U))))
- fvm::laplacian(this->alpha_*this->rho_*this->nuEff(), U)
);
}
Code:
//- Return the deviatoric part of a tensor
template<class Cmpt>
inline Tensor<Cmpt> dev2(const Tensor<Cmpt>& t)
{
return t - SphericalTensor<Cmpt>::twoThirdsI*tr(t);
}
 Therefore we get for the dev2 operator: ![\left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I} \left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}](/Forums/vbLatex/img/8572c3a1658524aae8f748a9997e5ba1-1.gif) Resubstituting everything into divDevRhoReff we get: ![-\nabla \bullet \left\{\alpha \rho \nu_\text{eff}\left(
\left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right)\right\}
-\Delta(\alpha \rho \nu_\text{eff} \textbf{U}) -\nabla \bullet \left\{\alpha \rho \nu_\text{eff}\left(
\left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right)\right\}
-\Delta(\alpha \rho \nu_\text{eff} \textbf{U})](/Forums/vbLatex/img/606ff8ab30aa0219cf2dd3c056724f60-1.gif) 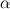 is the phase fraction and the negative signs come from the fact that the shear-rate tensor stand on the left hand side in the equation. is the phase fraction and the negative signs come from the fact that the shear-rate tensor stand on the left hand side in the equation.  is the dynamic viscosity and based on the fact that I assume it to be constant (density constant as well), we can take it out of the derivatives. The fraction is One here (single phase). Okay. Bringing everything to the RHS, dividing the equation by the density, assuming the kinematic viscosity to be constant and that we model only one phase ( is the dynamic viscosity and based on the fact that I assume it to be constant (density constant as well), we can take it out of the derivatives. The fraction is One here (single phase). Okay. Bringing everything to the RHS, dividing the equation by the density, assuming the kinematic viscosity to be constant and that we model only one phase (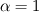 ) we get: ) we get:![+\nu_\text{eff} \Delta\textbf{U}
+\nu_\text{eff} \nabla \bullet \left\{\left(
\left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right)\right\} +\nu_\text{eff} \Delta\textbf{U}
+\nu_\text{eff} \nabla \bullet \left\{\left(
\left[(\nabla \otimes \textbf{U})^\text{T} \right] - \frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right)\right\}](/Forums/vbLatex/img/a69bb0619cd0c5ce7ce0f422fd123f46-1.gif) Just splitting the last term we get: ![+\nu_\text{eff} \Delta\textbf{U}
+\nu_\text{eff} \nabla \bullet
(\nabla \otimes \textbf{U})^\text{T} -
\nu_\text{eff} \nabla \bullet \left(\frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right) +\nu_\text{eff} \Delta\textbf{U}
+\nu_\text{eff} \nabla \bullet
(\nabla \otimes \textbf{U})^\text{T} -
\nu_\text{eff} \nabla \bullet \left(\frac{2}{3}\text{tr}\left[(\nabla \otimes \textbf{U})^\text{T}\right]\textbf{I}\right)](/Forums/vbLatex/img/9a9ae2e74c43020a26e55d131524e174-1.gif) By using your mathematics, the trace can be rewritten and we get the same equation as we had at the beginning and in fact it is similar to your equation in line 3 and the derivation is exact what you had (line #9, 10 and 12). In previous versions, the divDevReff function called the dev() operator. In version 4.x it calls dev2(). However, for incompressible cases - as you also said - the last term vanishes based on the continuity equation. Well, to be honest, it is my personal statement that I made that keeping that term (which is introduced by dev() or dev2()) is just for numerical stabilization of faster convergence because the term does not have to be zero in the numerical point of view. However, I could be wrong here. Why do I think so? In [11] there is a chapter about LU-Decomposing and error estimation and improving of solutions. Here, they mention to track (or at least calculate) the error and improve the solution based on the error. Which is somehow similar here. However, if we do not combine the terms like you did, it is more or less obvious that dev2 has a higher impact than dev based on the three terms. I think the main part here might come from explicit and implicit treatment because the gradient could not be treated implicitly and the argument of dev or dev2 is in fact explicit. Your mathematical re-arrangement is valid - of course but maybe they do not merge the terms based on that. This reminds me somehow to the stress implementation which is done in FOAM. Compressible in FOAM and dev2 I think I can skip this because we get the same equation as above and exact the same like you have. The outcome is that in 4.x (and 3.x?) the shear-rate tensors are identically (but you already proofed it). Summing up for previous FOAM versions In my book, chapter 9, I made this derivations for 2.3.x (maybe a bit more clear). Here, we had both operators (as you also stated). However, the dev() operator (for me) returns the real deviatoric part. I am not sure if we should really say that dev2() returns the deviatoric part because (I might be wrong here) as far as I know the deviatoric part of a tensor is always without the hydrostatic (spherical) one which is defined as:  but even in the Source code they mention that it is the deviatoric part. Maybe for compressible fluids the deviatoric part is two thirds, don't know but maybe you know it better. The literatures are given here: http://www.holzmann-cfd.de/index.php/en/literature I am not sure if this clarify it now? For me, it was new that you put the last two terms together - never saw this in my literature before but it is correct, definitely.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#57 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Hi Tobi,
Thank you for your clear check. You probably have rigth about the "stabilization" term. I don't get all, but I suppose your guess is a good one. Thank you. Sorry, again, for the bad start. I apologize. Zarox |
|
|
|

|
|
|
|
|
#59 |
|
Member
Emeline Noel
Join Date: Dec 2013
Location: Paris
Posts: 31
Rep Power: 13  |
Dear Tobi,
I don't get all about the stabilization term, how it's work with the LU decomposition and so on. I used to work on a Poisson solver with BiCGStab and Multigrid solver and so on, but I am not expert in the math. A least not enough to get the clear effect of the additional term on the convergence. However, I think that your feeling is good. Have a nice day/night whatever time line you are! Zarox |
|
|
|

|
|
|
|
|
#60 |
|
New Member
Wahahawsw
Join Date: Feb 2017
Posts: 6
Rep Power: 9  |
I have same problem with the reactingFoam. As i have implemented my thermophysicalModel.
I have a few problems as following : 1: In the UEqn.H, how is turbulence->divDevRhoReff() calculated in the code? 2: In the EEqn.H, how is turbulence->alphaEff() and reaction->Sh() calculated in the code? 3: In the YEqn.H, how is turbulence->muEff() and reaction->R(Yi) calculated in the code? As i can't find their code, I am troubled by these problems. I want to know how these terms are calculated . Thank you very much in advance if you have some ideas about those problems. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Calculating Vorticity | David | CFX | 28 | October 29, 2017 19:02 |
| Calculating Drag | Ajay Rao | FLUENT | 8 | February 15, 2010 10:15 |
| what is Fluent calculating? | tomek | FLUENT | 1 | July 24, 2006 18:52 |
| errors in calculating | ustcer | FLUENT | 1 | April 4, 2004 14:08 |
| Calculating Coefficients | shabah | CFX | 2 | June 19, 2001 00:59 |