 |
|
|
[Sponsors] | |||||
Interfoam: Constitutive equation and shear stresses |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Carlos Arboleda
Join Date: Jan 2016
Posts: 2
Rep Power: 0  |
Dear foamers,
I am trying to understand some terms in the interfoam solver namely: - fvm::laplacian(muEff, U) - (fvc::grad(U) & fvc::grad(muEff)) To my current understanding, this terms arise from the constitutive equation of a Newtonian isotropic fluid and can be written disregarding the minus(-) sign as 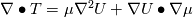 or in index notation or in index notation 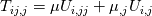 where the comma (',') subscript refers to the differentiation. where the comma (',') subscript refers to the differentiation. The constitutive relation states that 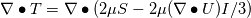 where 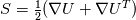 . .Due to incompresibility, 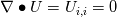 , thus: , thus: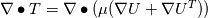 In index notation: 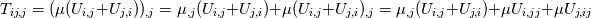 The last term 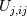 can be written as can be written as 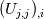 and and 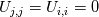 . . Leaving us with a different result than the one coded in interfoam: 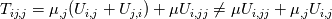 or in vector notation: 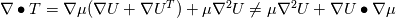 This is the result I have so far but it is not the accepted formulation implemented in the interfoam solver, thus my questions: Is there a mistake in my reasoning? Have I forgotten a term or a previous step? What are the missing steps to achieve the formulation in interfoam? Thanks in advance for any hint you can provide me. Carlos Last edited by carboleda; July 12, 2021 at 06:50. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Carlos Arboleda
Join Date: Jan 2016
Posts: 2
Rep Power: 0  |
||
|
|

|
|
 |
| Tags |
| interfoam, shear stress, tensor |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Shear Stress Calculation in the flow. | auburnuser | FLOW-3D | 11 | May 12, 2018 14:49 |
| How to add the transportation equation of insoluble surfactant to interFoam? | Hsin | OpenFOAM Programming & Development | 0 | December 25, 2016 23:21 |
| TKE budget equation in LES | doctorWho | Main CFD Forum | 3 | March 12, 2014 12:27 |
| Derivation of Momentum Equation in Integral Form | Demonwolf | Main CFD Forum | 2 | October 29, 2009 20:53 |
| Calculating average wall shear? | Joe | CFX | 3 | March 17, 2007 10:42 |