 |
|
|
[Sponsors] | |||||
Pressure boundary conditions, simpleFoam, plate near a wall |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Hi all,
I am trying to solve steady, laminar, shear flow about a plate near a wall. The aim is to understand how separation and flow reversal occur as viscosity changes and the gap between the plate and wall decreases. I am using simpleFoam, however cannot work out which BCs to use. I have searched the internet and literature high and low and cannot get to a suitable answer. - Here I am not sure that the zeroGradient condition holds because nu is non-zero/relatively large and with the plate inclined towards, and close to the wall, the usual arguments of du/dx = 0 etc do not follow. As a result I feel as though the way forward is to have dp/dn = nu d2v/dn2 on the lower wall and plate boundaries. Is there a way of achieving this in OF and simpleFoam? or should I use a different solver? The other BCs are: - Plate: U = zeroGradient; p = ??? - Wall: U = U_w (positive or negaitve_; p = ??? - Inlet: U = U_w + y; p = zeroGradient - Outlet: U = zeroGradient; p = 0 - Upper: U = U_W + y_max; p = zeroGradient Any help or advice is appreciated! |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Carlo_P
Join Date: May 2019
Location: Italy
Posts: 176
Rep Power: 8  |
Hey,
I corrected your BCs: -Plate: U = zeroGradient; p = zeroGradient - Wall: U = U_w (positive or negaitve_; p = zeroGradient - Inlet: U = U_w + y; p = zeroGradient - Outlet: U = zeroGradient; p = 0 - Upper: U = U_W + y_max; p = zeroGradient but..I have a question: how you can calculate the separation using a laminar flow? |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Thanks Carlo_P for your time and response.
My supervisor and I are not convinced that the zeroGradient condition holds in this case though due to the presence of the plate and the viscousity of the fluid. I have read the other threads on here and I am not sure the justification there hold here for either the wall or the plate. Could you explain why the zeroGradient would be the correct choice? As for separation, why would laminar flow be an issue? In theory it is admissible in a laminar boundary layer, and we do see the typical characteristics with flow reversal about the plate, eddies forming below the plate and in the wake, and adverse pressure gradients in the cases we've run. Last edited by RyArPa; October 22, 2019 at 12:44. Reason: Spelling error |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
In addition, out of interest - is there a way to set a boundary condition of dp/dn = nu d^2v/dn^2 in OF?
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Ruiyan Chen
Join Date: Jul 2016
Location: Hangzhou, China
Posts: 162
Rep Power: 10  |
I think it would be better if you put up a figure that shows the domain the boundaries. I'm kind of interested in this, is the plate parallel to the wall and you decrease the distance between them to see what are the effects?
zeroGradient for pressure is pretty straightforward, if you have a pressure gradient near a wall boundary, there will be flow penetrating it, which is physically not possible. You mentioned something about very large fluid viscosity, but that should have nothing to do with pressure. I see that you are using zeroGradient for velocity of the plate, is the plate moving? Anyway, a simple figure would help a lot here. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Thanks for your interest and advice cryabroad - that is helpful, and it is a fascinating problem when you get into it!
Here is a figure. - The plate is inclined to the wall, with varying inclination for different scenarios. - We are in a frame of reference fixed on the plate, so it is static but the wall is moving relative to the plate in either an upstream or downstream direction (giving a positive or negative wall velocity) such that the inlet velocity profile is: U = Uw + y, with the wall at y = 0, and the plate some varying distance from the wall. The plate U BC was an error - it is no-slip. Sorry. As for zeroGradient pressure, my understanding was that a pressure gradient near the wall would be equivalent to flow penetrating it, however, from the equations we keep landing at: dp/dn = nu d^2v/dn^2 as the correct condition on the wall... I can't quite resolve this. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Ruiyan Chen
Join Date: Jul 2016
Location: Hangzhou, China
Posts: 162
Rep Power: 10  |
Okay now I get the point. I think the problem may come from the reference frame you are working with. I guess you have to add certain terms in the equation to make the reference frame work, and that's probably why you end up with additional terms. Can you share the derivation of the dp/dn term you mentioned? I think this is where the confusion is. I still think the pressure boundary condition should be zeroGradient, because there should be no additional acceleration term (pressure gradient is basically acceleration) if things are moving at constant speeds in your original problem (before you change the reference frame).
Additionally, do check if OpenFOAM has built-in moving reference frame (MRF) modules. I think it does, at least I know Fluent has it. Such built-in modules should be designed in a way that the user doesn't need to worry about things related to MRF, in that case the pressure boundary condition should definitely be zeroGradient on the wall. |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
[Duplicated post]
Last edited by RyArPa; October 25, 2019 at 05:20. Reason: Accidental duplication of posts - see below |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Thanks that its helpful advice - I will look into it!
 As for the derivation of the BC for pressure (working for the wall, for ease, where the normal is in the 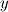 -axis), I am solving the continuity and momentum equations in 2D: -axis), I am solving the continuity and momentum equations in 2D:(1)  (2)  (3)  The velocity BCs on the wall are:  , which is constant for , which is constant for  (such that (such that  ); and ); and  which is constant in which is constant in  (but not necessarily in (but not necessarily in 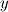 ) )Hence,  such that by (1): such that by (1):  Plugging all of this into (3) we get:  (although (although  and and  , the overall profile of , the overall profile of  is unknown, hence, for example, there could be quadratic contributions such that the above all holds - in fact such contributions are likely given the locality of the plate to the wall and the effect on the fluid flow as a result of its presence). is unknown, hence, for example, there could be quadratic contributions such that the above all holds - in fact such contributions are likely given the locality of the plate to the wall and the effect on the fluid flow as a result of its presence).As a result this makes the BC:  . .This all leaves me with three questions that I am pondering/looking in to... (which I will continue to mull over!!!): (1) does the above mean that the zeroGradient condition is inappropriate for pressure? (2) if so, what alternatives/methods are there available in OF to resolve this? (3) if it is appropriate, why? are there nuances in OF's implementation of the SIMPLE algorithm that I have not considered or perhaps the mathematics above incorrect? |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Ruiyan Chen
Join Date: Jul 2016
Location: Hangzhou, China
Posts: 162
Rep Power: 10  |
Sorry for my late response, got caught up in some projects.
I went through your derivation, and I'm not sure if the second inequality in this expression holds,  . We don't know what the gradient of wall normal velocity is before we solve the problem, why the inequality? The correct way of doing this is to assume . We don't know what the gradient of wall normal velocity is before we solve the problem, why the inequality? The correct way of doing this is to assume  and go from there. and go from there.For boundary value problems, one can only specify one type of boundary condition for one variable at one boundary. In this case,  at the wall is sufficient for at the wall is sufficient for  , to state , to state  at the wall is an overconstraint I think. For example, just from the above expression, at the wall is an overconstraint I think. For example, just from the above expression,  can be a linear function with respect to the wall distance and satisfies the constraint of can be a linear function with respect to the wall distance and satisfies the constraint of  at the wall. In such case, at the wall. In such case,  . Anyway, I think searching for MRF in OpenFOAM should be a good option for your case. . Anyway, I think searching for MRF in OpenFOAM should be a good option for your case.
|
|
|
|

|
|
|
|
|
#11 |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Quote:
Hi cryabroad, sorry for the delay (I have been away on leave). One slight confusion, it's my fault for not being clearer - I am not imposing  , rather I probably should have said , rather I probably should have said  , where , where 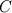 is some constant that may or may not be 0. Hence, is some constant that may or may not be 0. Hence,  is calculated at the boundary, for which is calculated at the boundary, for which 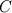 is found rather than set. If anything, forcing is found rather than set. If anything, forcing  over-constrains the problem in my mind? over-constrains the problem in my mind?
|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Ruiyan Chen
Join Date: Jul 2016
Location: Hangzhou, China
Posts: 162
Rep Power: 10  |
I think we both agree that the first equality holds, which is
 . The problem is how do we go from here. . The problem is how do we go from here.As I mentioned, for such a boundary value problem, to state anything associated with  when we already establish the fact that when we already establish the fact that  is not right, and it does over-constrain the problem. Even if you are assuming is not right, and it does over-constrain the problem. Even if you are assuming  , that is not right in my mind. , that is not right in my mind.However, in fluid mechanics pressure and velocity are coupled. When you specify a boundary condition for pressure/velocity, it implicitly constrains the velocity/pressure (in one form or the other) at the same boudary, which looks like you are over-constraining the problem. In other words, it is not that the  condition is forced by us, it is forced by continuity. Again, I do think that for an accelerating or decelerating system this is NOT the case, and more derivations have to be done to figure out the correct boundary conditions. But for the system you are considering (which is at constant speed), I think it should be just as simple as a normal zero pressure gradient condition. condition is forced by us, it is forced by continuity. Again, I do think that for an accelerating or decelerating system this is NOT the case, and more derivations have to be done to figure out the correct boundary conditions. But for the system you are considering (which is at constant speed), I think it should be just as simple as a normal zero pressure gradient condition.
|
|
|
|

|
|
|
|
|
#13 | |
|
New Member
Ryan
Join Date: Oct 2019
Posts: 8
Rep Power: 7  |
Thanks for your time on this - I think I understand what you are saying now and it is becoming clearer in my mind. I still have a reservation though.
You say: Quote:
To clarify: I am not looking to say that  is definitely some constant and thus imposed that as a BC alongside a pressure BC and another velocity BC, since this would over constrain the problem. is definitely some constant and thus imposed that as a BC alongside a pressure BC and another velocity BC, since this would over constrain the problem. Rather,  could be constant, or zero, or something else, we don't know. Hence I am looking for a pressure BC such that could be constant, or zero, or something else, we don't know. Hence I am looking for a pressure BC such that  on the boundary. on the boundary. I think is mathematically valid since with a zeroGradient BC we have  and are imposing a value on and are imposing a value on  through the pressure coupling. Which is what I would like to do here, but for a potentially non-zero value. through the pressure coupling. Which is what I would like to do here, but for a potentially non-zero value.
|
||
|
|

|
||
 |
| Tags |
| simplefoam pressure bc |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Question about adaptive timestepping | Guille1811 | CFX | 25 | November 12, 2017 18:38 |
| Wrong multiphase flow at rotating interface | Sanyo | CFX | 14 | February 7, 2017 18:19 |
| Multiphase flow - incorrect velocity on inlet | Mike_Tom | CFX | 6 | September 29, 2016 02:27 |
| interFoam (HELYX-OS) pressure boundary conditions | SFr | OpenFOAM Running, Solving & CFD | 8 | June 23, 2016 17:36 |
| Basic Nozzle-Expander Design | karmavatar | CFX | 20 | March 20, 2016 09:44 |