 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 16  |
I am implementing the Artificial Compressibility (AC) and Fractional-Step Pressure Projection (FS-PP) method into OpenFOAM. For laminar flows, they work well and I can validate them against benchmark cases. Next, I wanted to add turbulence and added the turbulence->divDevReff() object, which in turn is adding the viscous and Reynolds stresses. So I removed the laplacian operator from my momentum equation but then get different results.
For the AC method, it seems my results are correct when I add the laplacian to the momentum equation, but for the FS-PP method, it seems to work only if I remove the same operator. If I reverse this, i.e. remove the laplacian from the AC method and add it to the FS-PP method, I am getting incorrect results. I am testing the couette flow as a test case and I am adding the dual time stepping to the AC method to get a correct time behaviour. This is, for the moment, a laminar test case and turbulence is switched off. Solving the AC method with the following momentum equation: Code:
fvVectorMatrix UEqn ( fvm::ddt(U) + fvm::div(phi, U) + turbulence->divDevReff(U) == - fvm::Sp(dualTime.SpCoefficient(), U) + fvc::Sp(dualTime.SuCoefficient(), dualTime.Su()) ); 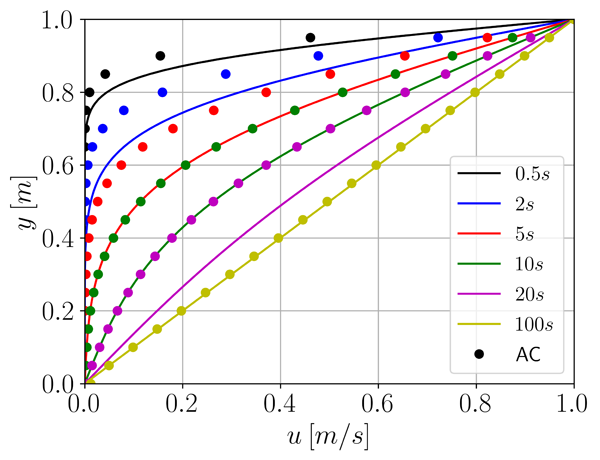 If I change the momentum equation to include the viscous term, i.e. solving Code:
fvVectorMatrix UEqn ( fvm::ddt(U) + fvm::div(phi, U) - fvm::laplacian(turbulence->nuEff(), U) + turbulence->divDevReff(U) == - fvm::Sp(dualTime.SpCoefficient(), U) + fvc::Sp(dualTime.SuCoefficient(), dualTime.Su()) ); 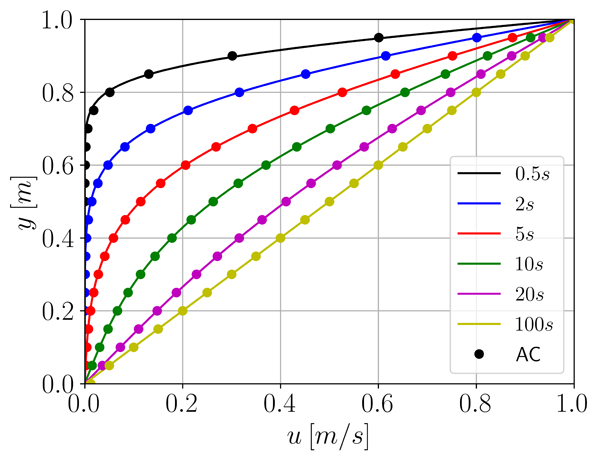 So it seems that the correct solution is obtained including the laplacian (which is odd as the turbulence->difDevReff() is including the same term. For the FS-PP method, it is the opposite behaviour, i.e. if I solve the momentum equation without laplacian, i.e. Code:
fvVectorMatrix UEqn ( fvm::ddt(U) + fvm::div(phi, U) + turbulence->divDevReff(U) ); 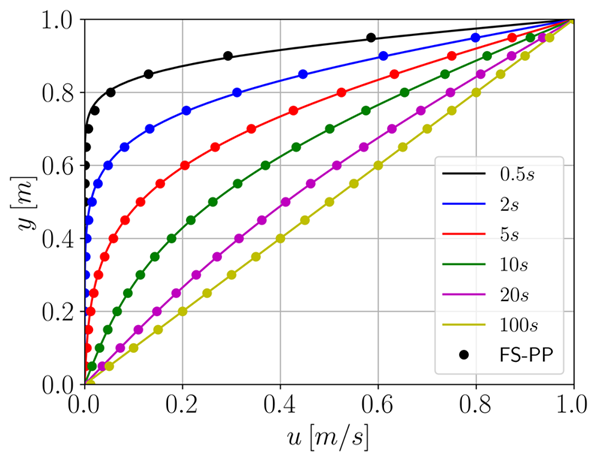 and if I include the laplacian, i.e. solving Code:
fvVectorMatrix UEqn ( fvm::ddt(U) + fvm::div(phi, U) - fvm::laplacian(turbulence->nuEff(), U) + turbulence->divDevReff(U) ); 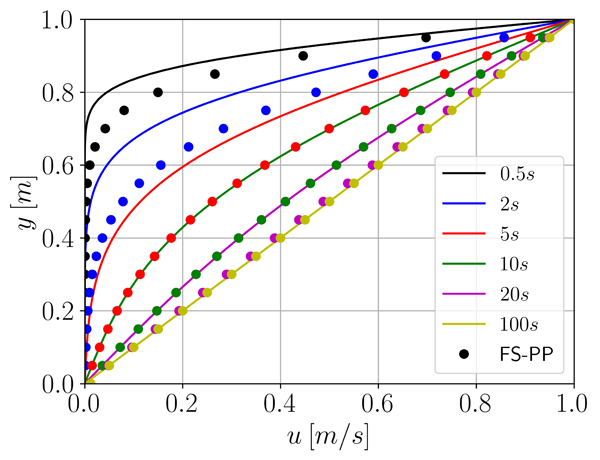 which demonstrates that the correct behaviour is seemingly obtained with the laplacian for the AC method but without for the FS-PP method. It seems that the FS-PP implementation is correct as the laplacian term is included only once and that there is something wrong with the AC method. The source term in the AC method is simply the contribution of the real time derivative, i.e. in the simplest case the backward Euler scheme as (U^n+1 - U^n) / dt. Here, both Sp and Su coefficients are 1/dt and Su itself is U^n. Substituting that back into the momentum equation will reconstruct the time derivative as given above. Any ideas what could cause this problem? Last edited by t.teschner; September 5, 2020 at 14:57. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Radiation Modeling Using Discrete Ordinates Method and Parallel Solver | malicemethods | FLUENT | 3 | May 25, 2018 15:25 |
| fluent divergence for no reason | sufjanst | FLUENT | 2 | March 23, 2016 17:08 |
| thobois class engineTopoChangerMesh error | Peter_600 | OpenFOAM | 4 | August 2, 2014 10:52 |
| Working directory via command line | Luiz | CFX | 4 | March 6, 2011 21:02 |
| why the solver reject it? Anyone with experience? | bearcat | CFX | 6 | April 28, 2008 15:08 |