 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Knut Olafson
Join Date: Jun 2019
Posts: 6
Rep Power: 7  |
Hey Guys,
I have some troubles in finding ways to enable implicit solving for a WaveEquation with material derivatives in OF. I consider a WaveEq in 3D for a volscalarfield u(x,t) with material derivatives in time: 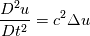 with with 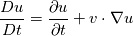 . .Now I may have two options: solving this PDE with second order time derivatives or writing a system of two PDEs with first order time derivatives. In the first case I have some mixed derivatives like 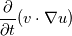 . Since I want to solve the equation fully implicit, i now have problems with Openfoam for wanting to build up a fvmatrix from a fvmatrix (i.e. fvm::ddt(fvm::div(phi,u)) ). Even if I would solve the inner term explicitly (i.e. fvm::ddt(fvc::div(phi,u)) ) i would get troubles by adding the non-mixed terms (i.e. fvm::d2dt2(u) and fvm::laplacian(u)) because OF would not know for which volscalarfield he has to solve the equation (i.e. u or fvc::div(phi,u) ). . Since I want to solve the equation fully implicit, i now have problems with Openfoam for wanting to build up a fvmatrix from a fvmatrix (i.e. fvm::ddt(fvm::div(phi,u)) ). Even if I would solve the inner term explicitly (i.e. fvm::ddt(fvc::div(phi,u)) ) i would get troubles by adding the non-mixed terms (i.e. fvm::d2dt2(u) and fvm::laplacian(u)) because OF would not know for which volscalarfield he has to solve the equation (i.e. u or fvc::div(phi,u) ).In the second case the problem is quite the same: by adding a second volscalarfield i get a system like 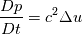 , , 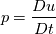 . For solving the first equation I have the same problem: if i want to discretize fully implicit OF does not know for which volscalarfield he has to solve (i.e. p or u). . For solving the first equation I have the same problem: if i want to discretize fully implicit OF does not know for which volscalarfield he has to solve (i.e. p or u).Does anybody have an Idea how i could manage this? I also tried to implement a implicit RungeKutta scheme for the time derivatives and solving in each time step with a handwritten newton/fixed point/regula falsi/whatever approximation. But here I have the same problems in enabling implicit spatial discretization, too. Thanks a lot for your thoughts! Greetings, Knut |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Knut Olafson
Join Date: Jun 2019
Posts: 6
Rep Power: 7  |
Push: does anybody have any ideas?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 616
Rep Power: 16  |
There a second order time schemes https://cfd.direct/openfoam/user-guide/v6-fvschemes/
However apparently only euler |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Knut Olafson
Join Date: Jun 2019
Posts: 6
Rep Power: 7  |
Yes. Second Order time derivative with implicit euler. But I already tried this (see my first post). The problem is, with second order material derivatives there are mixed derivatives as well. And they can't be solved fully implicit as one would need to build up a fvmatrix from a fvmatrix (and not from a scalarfield).
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 616
Rep Power: 16  |
What do you mean with fully implicit. When you have time derivatives you always have a source like term resulting from the past time step
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
Knut Olafson
Join Date: Jun 2019
Posts: 6
Rep Power: 7  |
I mean that i.e. in
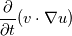 for the inner spatial derivative (gradient), the discretization should not explicitly use the source term from the last timestep but from the new time step (which is not yet computed). Then we would get a system which is to solve. for the inner spatial derivative (gradient), the discretization should not explicitly use the source term from the last timestep but from the new time step (which is not yet computed). Then we would get a system which is to solve.And this is somehow my question. If I use fvm::ddt(fvc::div(phi,u)) in OF, does the system use new (not yet calculated) values to discretize the gradient, or just old ones? As I understood it, just the old ones. But something like fvm::ddt(fvm::div(phi,u)) (which is not possible in OF) should use the new ones. And if it is like this, how can I build up something like fvm::ddt(fvm::div(phi,u)) in OF? |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 616
Rep Power: 16  |
Quote:
You can discretize 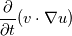 using a first order Euler discretization. Doing a finite volume discretization of the above term you get: using a first order Euler discretization. Doing a finite volume discretization of the above term you get: 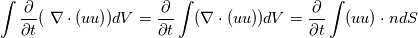 . . The last expression can be expressed using a first order euler (you can also use higher order discretization of course) by: Code:
1.0/mesh().time().deltaT() * ( fvm::div(phi,U) - fvc::div(phi,U) ) |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Segmentation fault when using reactingFOAM for Fluids | Tommy Floessner | OpenFOAM Running, Solving & CFD | 4 | April 22, 2018 13:30 |
| chtMultiRegionSimpleFoam turbulent case | Aditya Patil | OpenFOAM Running, Solving & CFD | 6 | April 24, 2017 23:13 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Unstabil Simulation with chtMultiRegionFoam | mbay101 | OpenFOAM Running, Solving & CFD | 13 | December 28, 2013 14:12 |
| calculation stops after few time steps | sivakumar | OpenFOAM Running, Solving & CFD | 7 | March 17, 2013 07:37 |