 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Maximus Arelius
Join Date: Jan 2017
Location: Morocco
Posts: 36
Rep Power: 9  |
Hi OF Community Members,
Greetings! I need your expertise with the following problem. I was going through Prof. Jasak's paper "Multi-dimensional simulation of thermal non-equilibrium channel flow!" where a different type of pressure equation was formulated as opposed to what is used in the variable density/compressible solvers of OpenFOAM. https://www.sciencedirect.com/scienc...0193220900192X In it the compressible/multiphase continuity is split from 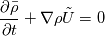 to  Now considering compressible flow only  . .Hence material derivative is expanded as  . .It would be really helpful if you could share some thoughts on the following questions: 1.For a variable density flow with face flux as the Mass flux 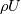 at face, the above equation will have volumetric flux phi, which is to be used to find mass flux by interpolation of density to the faces. at face, the above equation will have volumetric flux phi, which is to be used to find mass flux by interpolation of density to the faces.Where should this in a (say) compressible solver be done( just after phi update or elsewhere)? 2.If we treat the pressure terms on the RHS i.e  , temporal term and source term , temporal term and source term  so as to impart numerical stability, then following phi = phi - pEqn.Flux() How will one update the volumetric fluxes as the pEqn now has a new convective term on the RHS following Dr.Jasak Thesis? so as to impart numerical stability, then following phi = phi - pEqn.Flux() How will one update the volumetric fluxes as the pEqn now has a new convective term on the RHS following Dr.Jasak Thesis? 3.How is this kind of formulation different(physics wise) from that used in the regular openfoam solvers i.e.  Note: The  are used for a Favre averaged framework. Also the are used for a Favre averaged framework. Also the  is treated as done in incompressible solvers in OF. is treated as done in incompressible solvers in OF.Correct me if I am wrong anywhere! Thanks in advance  
__________________
-- 🃏Maximus🃏 Last edited by godfatherBond; May 7, 2018 at 00:36. |
|
|
|

|
|
|
|
|
#2 | |
|
Member
Maximus Arelius
Join Date: Jan 2017
Location: Morocco
Posts: 36
Rep Power: 9  |
Quote:
    
__________________
-- 🃏Maximus🃏 Last edited by godfatherBond; April 30, 2018 at 01:07. |
||
|
|

|
||
|
|
|
#3 |
|
Member
Maximus Arelius
Join Date: Jan 2017
Location: Morocco
Posts: 36
Rep Power: 9  |
Hi FOAMers,
Still looking for an explanation. It would be beneficial if you could spare some time and have a look into it. Thanks
__________________
-- 🃏Maximus🃏 |
|
|
|

|
|
 |
| Tags |
| cfd - post, openfoam |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| question regarding LES of pipe flow - pimpleFoam | Dan1788 | OpenFOAM Running, Solving & CFD | 37 | December 26, 2017 15:42 |
| Pressure Outlet Guage pressure | Mohsin | FLUENT | 36 | April 29, 2016 18:16 |
| The correction on pressure equation of SIMPLE algorithm in MRFSimpleFOAM solver | renyun0511 | OpenFOAM Running, Solving & CFD | 0 | November 10, 2010 02:47 |
| How to add correcting pressure equation in SIMPLE of MRFSimpleFOAM? | renyun0511 | OpenFOAM Programming & Development | 0 | November 4, 2010 02:38 |
| Pressure enigma. | Sara | Main CFD Forum | 22 | July 30, 2009 05:46 |