 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Albin Lindskog
Join Date: Dec 2017
Posts: 8
Rep Power: 9  |
Hello,
I am creating a custom solver that is based around the following equation:  where a, b and c are constants. v and y are both scalars. y is known and v is the variable I'm solving for. My approach is to implement a generic solution (3D) and introduce the one-dimensional condition by defining all side patches as empty. As such I am trying to implement the following equation in my solver: 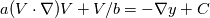 Where V and C instead are vectors. However I am struggling to do so. Is this the recommended/correct approach to my problem? How would I implement equation 2 in my Solver? Are there any resources describing this part of OpenFOAM-development? |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Albin Lindskog
Join Date: Dec 2017
Posts: 8
Rep Power: 9  |
I've made an attempt to implement the equation
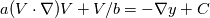 based on icoFoam: Code:
surfaceScalarField phi = fvc::interpolate(V) & mesh.Sf();
fvVectorMatrix VEqn
(
a * fvm::div(phi, V)
+ fvm::Sp((1/b), V)
);
solve(VEqn == -fvc::grad(y) + C);
The solution produced are however non-physical. Is there something I've overlooked or misunderstood? Thanks in advance, Dharoc |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Hello,
The main thing is that if you create an almost 1 dimensional grid with suitable boundary conditions. You can still run OpenFOAM codes in 1 dimensional. I mean there is no 1 dimensional coding approach. The second thing that I wanted to mention and you might probably find it helpful is trying to adapt OpenFOAM momentum (UEqn.H) to your case by adding and excluding terms. Easily, you can make it compatible with your case. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Albin Lindskog
Join Date: Dec 2017
Posts: 8
Rep Power: 9  |
Hello babakflame, thank you for your reply. That is exactly how I've approached the problem so far, so it's nice to know I've taken the right approach.
I've also identified the issue I described in the second post i this thread. The problem was not my implementation of the equation, but rather with the boundary conditions for the y-field. So far now are things looking promising. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Albin Lindskog
Join Date: Dec 2017
Posts: 8
Rep Power: 9  |
Hello again!
I'm stuck with the same problem, albeit with another equation. I'm trying to implement:  where V is a volVectorField and a and b are volScalarFields. Does anyone have any pointers? Last edited by Dharoc; May 12, 2018 at 09:24. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Albin Lindskog
Join Date: Dec 2017
Posts: 8
Rep Power: 9  |
I've not made any progress. Just to clarify, I'm trying to implement the following one-dimensional equation, where a is the unknown I'm solvning for:
 By generalising it to the following three-dimensional equation and using empty boundary conditions to make it one-dimensional.  Is this not the correct approach in this case? Last edited by Dharoc; May 12, 2018 at 11:56. |
|
|
|

|
|
 |
| Tags |
| 1-d, development, equation, generalising, generalizing |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| rotational and inviscid | Mike | Main CFD Forum | 40 | November 9, 2023 07:03 |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 06:21 |
| Some problem of "Qcriterion.mcr& | yuyuxuan | Tecplot | 9 | February 12, 2016 04:27 |
| Need help:about energy equation in CFX | Stein | CFX | 4 | July 2, 2009 23:31 |
| Diffusion Equation | izardy amiruddin | Main CFD Forum | 2 | July 4, 2002 09:14 |