 |
|
|
[Sponsors] | |||||
source term modification in poisson equation does not affect results |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Fellows
I have written a simple poissonFoam code which contains a source term in form of a 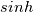 function. function.The code solves this equation:  . .I have attached the code and a sample case. I have assigned different values for 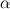 and and 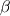 , however, I get the following distribution every time. Do u have any idea why this happens and how would I be able to see the effect of , however, I get the following distribution every time. Do u have any idea why this happens and how would I be able to see the effect of 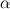 and and 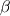 on the results? on the results?PS: in the attached picture, phi is nondimensionalized by the value at the left boundary of sample case (alpha3.tar.gz) and x is non-dimensionalized by 30e-09. Last edited by babakflame; August 17, 2016 at 23:08. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Fellows
I have posted the text of my poissonFoam.c and createFields.H files below. Probably, I have a problem in clearly defining my source term: poissonFoam.C : Code:
#include "fvCFD.H"
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
int main(int argc, char *argv[])
{
#include "setRootCase.H"
#include "createTime.H"
#include "createMesh.H"
#include "createFields.H"
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
Info<< "\nStarting iteration loop\n" << endl;
while (runTime.loop())
{
Info<< "Iteration = " << runTime.timeName() << nl << endl;
solve
(
fvm::laplacian(phi) - beta*sinh(alpha*phi)
);
runTime.write();
Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
<< " ClockTime = " << runTime.elapsedClockTime() << " s"
<< nl << endl;
}
Info<< "End\n" << endl;
return 0;
}
Code:
Info<< "Reading physicalProperties\n" << endl;
IOdictionary physicalProperties
(
IOobject
(
"physicalProperties",
runTime.constant(),
mesh,
IOobject::MUST_READ_IF_MODIFIED,
IOobject::NO_WRITE
)
);
dimensionedScalar alpha
(
physicalProperties.lookup("alpha")
);
dimensionedScalar beta
(
physicalProperties.lookup("beta")
);
Info<< "Reading field phi\n" << endl;
volScalarField phi
(
IOobject
(
"phi",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
Any hint is kindly appreciated. Last edited by babakflame; August 18, 2016 at 01:36. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Fellows
I figured out my problem. It was on the value of Phi which actually made the hyperbolic function be in the location near zero. BTW: the poisson solver works perfectly. feel free to use it. 
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Fellows
I am experiencing a weird issue in dealing with poisson equation in OpenFoam. In the first post of this thread you can see that I have written a poissonFoam code that works with openFoam 2.1.x. This code solves the following relation:  Actually, I am interested in solving above equation in one dimensional which in my grid would be from left wall to right wall. My issue is with the grids. If I use a rectangular shaped grid with known and fixed values for 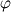 on left and right boundaries, the result is a linear distribution for on left and right boundaries, the result is a linear distribution for 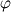 . The linear distribution mathematically happens merely when the source term in poisson equation is zero (in my case . The linear distribution mathematically happens merely when the source term in poisson equation is zero (in my case  ). But my source term is not zero. ). But my source term is not zero. However, if the grid be a sector with the angle of  , then the resulting distribution for , then the resulting distribution for 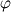 is an exponential distribution. is an exponential distribution. I have attached the grid types with the achieved distribution for 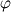 . . As you can see from the figures the value of 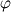 at left wall is 25.4e-03 and on the right wall is 0. at left wall is 25.4e-03 and on the right wall is 0.Actually, I am interested in solving the above poisson equation in 1 dimensional. So, using a sector (even with 1 degree) is somehow unphysical for me. Has some body else experienced sth similar to me? or any hint on this weird experience?   Is there any way to solve above equation on rectangular-shaped grid? You have my solver above, you can try this by yourself and see what happens.  |
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hello Bobi,
I am not 100% sure but if we would solve the simple laplace equation for a disc (or wedge) we would observe the same result. The analytical solution for the temperature equation within a cylinder is a logarithmic law (not linear). So I think everything is okay with your calculation.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Hey Tobi
Many thanks for your reply. Let me explain this a little further. I am interested in solving equation  in 1 dimensional situation with non-zero value at left side and zero value at right hand side. In one dimensional I have: in 1 dimensional situation with non-zero value at left side and zero value at right hand side. In one dimensional I have: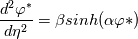 Here  is the non-dimensional coordinate and is the non-dimensional coordinate and  is the non-dimensional variable present in poisson equation. is the non-dimensional variable present in poisson equation. Here, 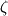 is the value of the left wall used to non-dimesionalize the is the value of the left wall used to non-dimesionalize the 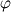 variable. variable. Since the right boundary is zero, by integrating twice, the above non-dimesional equation gives the following solution: ![\varphi ^ \ast = \frac{4}{\alpha} tanh^{-1} \left[tanh (\frac {\alpha}{4}) exp (-\sqrt{\alpha \beta}\eta)\right] \varphi ^ \ast = \frac{4}{\alpha} tanh^{-1} \left[tanh (\frac {\alpha}{4}) exp (-\sqrt{\alpha \beta}\eta)\right]](/Forums/vbLatex/img/563849b3e28bce2966c02514b0685beb-1.gif) In the attached picture, you can observe the analytic solution: I am interested in solving above equation with  . .AFA I know, first of all, I need to make this equation dimensioanl in 1D and solve it with my solver. How ever, as I described in previous post, the results are based on grid shape which is weird for me. I mean If I use rectangular grid, result is linear and with curved left and right walls, result are exponential, however, I want the above solution seen in my results without grid shape dependancy     Am I missing sth here? By the way, the dimensional equation which I am solving becomes as follows: 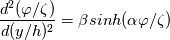 That is so weird for me  
Last edited by babakflame; September 7, 2016 at 01:15. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Fellows
The last thing that comes to my mind is that "probably there is a bug in O.F.2.1.x since It can not solve the Poisson equation (which is actually a Laplacian equation with source term) correctly on rectangle grids. My equation is  with left boundary condition 1 and right boundary condition zero would give the following exponential solution: ![\varphi ^ \ast = \frac{4}{\alpha} tanh^{-1} \left[tanh (\frac {\alpha}{4}) exp (-\sqrt{\alpha \beta}\eta)\right] \varphi ^ \ast = \frac{4}{\alpha} tanh^{-1} \left[tanh (\frac {\alpha}{4}) exp (-\sqrt{\alpha \beta}\eta)\right]](/Forums/vbLatex/img/563849b3e28bce2966c02514b0685beb-1.gif) However OF. 2.1.x gives linear disribution on roughly 1D rectangle grids |
|
|
|

|
|
|
|
|
#9 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
What came into mind is, what is alpha in your graph? Degrees? If yes, you have to transform this into Radian because foam work's with radian.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Dear Tobi
Many thanks for your reply and your time. Here, 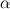 is just a coefficient that helps us to achieve different exponential distributions. Otherwise, all results are the same. is just a coefficient that helps us to achieve different exponential distributions. Otherwise, all results are the same.As it is seen in the attached figure, the following distributions are achieved by assuming different values for 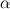 from 1 to 10 and from 1 to 10 and 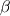 is just another constant considered to be equal to 10000. is just another constant considered to be equal to 10000. I just want to solve the following Poisson equation in 1 dimensional. This direction is assumed to be y direction between two boundaries. The value at left boundary is considered to be 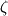 (could be any value) and right boundary is zero. (could be any value) and right boundary is zero.The non-dimensional equation is:  using these scales: 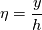 , ,  I found the dimensional equation as: 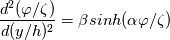 which finally becomes: 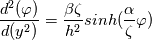 Here, I have used the value of  and and  and and 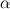 from 1 to 10. from 1 to 10.I have uploaded my results from the above curved grid. However, a roughly 1 D rectangular grid just gives linear lines. Even , my results from a curved grid are not fitted completely.   Here, in my results, the distance from the wall has been divided by 30e-09. PS: the distance between left and right boundary is considered to be 120e-09 m in my simulation. So 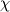 is from 0 to 4. is from 0 to 4.
|
|
|
|

|
|
|
|
|
#11 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear Bobi,
I am sorry for the last replay. I did not read everything and I saw that I already mentioned the stuff with the radian. Well I am not so familiar with non-dimensionalizing equations and using them in OpenFOAM. If the solution (integral) is correct, you should be able to get the same or closely the same values.
 To do that, I made a new field and stored it. The result of the source term is as expected (like the distribution you showed). The behavior is like a 1/x function but based on the small grid, the source term become like 1e-8 which will not decrease your quantity phi very much and that is the reason for the linear distribution. By the way, I was implementing the following equation:  Maybe the fact that I did not non-dimens. this equation lead to the behavior I got. In any case I have to say that I never did something like you are doing at the moment and therefore I am sorry not to provide you more information. Maybe Sergei (Zappo) or other more advanced and skilled people can help you in that topic. Good luck Bobi.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Thanks Tobi.
I will try to add transient term and check it that way too. 
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Sergei
Join Date: Dec 2009
Posts: 261
Rep Power: 22  |
But your plots "numeric/analytical" are qualitatively very similar. Unfortunatelly, I don't know why they don't match completely.
|
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
@Tobi
many thanks for your time Tobi. Actually, I made an elliptic code (without time derivative) that now applies the Poisson equation with 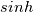 source term on rectangular grids correctly. source term on rectangular grids correctly.  But still a problem exists. But still a problem exists. @Sergei Thanks Sergei for looking at my question. Actually, I made a code that solves  on rectangular grids on rectangular grids Right Now, I am capable of achieving results up to the value of 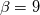 and the results seem fine. However, further increasing of and the results seem fine. However, further increasing of 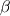 will result in the following error: will result in the following error:Code:
0 Foam::error::printStack(Foam::Ostream&) at ??:? #1 Foam::sigFpe::sigHandler(int) at ??:? #2 in "/lib/x86_64-linux-gnu/libc.so.6" #3 __sinh_finite in "/lib/x86_64-linux-gnu/libm.so.6" #4 sinh in "/lib/x86_64-linux-gnu/libm.so.6" #5 Foam::sinh(Foam::Field<double>&, Foam::UList<double> const&) at ??:? #6 at ??:? #7 at ??:? #8 at ??:? #9 __libc_start_main in "/lib/x86_64-linux-gnu/libc.so.6" #10 at ??:? Floating point exception (core dumped) Code:
volScalarField beta
(
IOobject
(
"beta",
runTime.timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh,
dimensionedScalar("beta", dimensionSet(0, -2, 0, 0, 0, 0, 0), scalar(12.0))
);
Info<< "Reading field phi\n" << endl;
volScalarField phi
(
IOobject
(
"phi",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
volScalarField tmp1
(
IOobject
(
"tmp1",
runTime.timeName(),
mesh,
IOobject::NO_READ,
IOobject::AUTO_WRITE
),
// Foam::sinh(alpha * phi)
1 * Foam::sinh(phi)
);
Code:
while (runTime.loop())
{
Info<< "Iteration = " << runTime.timeName() << nl << endl;
solve
(
fvm::laplacian(phi) - beta * sinh(phi)
// fvm::laplacian(phi) - beta * (phi + (1/6)*pow(phi,3) + (1/120)*pow(phi,5) + (1/362880)*pow(phi,9) + (1/39916800)*pow(phi,11))
);
runTime.write();
Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
<< " ClockTime = " << runTime.elapsedClockTime() << " s"
<< nl << endl;
}
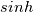 term as a summation of polynomials, but this did not remove the above error. term as a summation of polynomials, but this did not remove the above error.The following is my fvSolution and fvSchemes: Code:
laplacianSchemes
{
default Gauss linear corrected;
laplacian(phi) Gauss linear corrected;
}
Code:
phi
{
solver PCG;
preconditioner DIC;
tolerance 1e-11;
relTol 0.0;
}
|
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Sergei
Join Date: Dec 2009
Posts: 261
Rep Power: 22  |
||
|
|

|
|
|
|
|
#16 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
||
|
|

|
|
|
|
|
#17 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
based on the fact that you do not have a time derivation (this is somehow a limiter), you should underrelax your equation. For that you have to build the matrix first, relax it and then solve it. I am not sure if it will help but I think it should. If you increase the value of the quantity beta, your problem gets more stiff and your solution procedure has to be improved. That is my experience but I think Sergei can make a better statement. Good luck.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Thanks Tobi
 Your suggestion makes sense to me too. I will try it and provide the feedback.  Regards |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Bobby
Join Date: Oct 2012
Location: Michigan
Posts: 454
Rep Power: 16  |
Hey Tobi,
I built the matrix and did the relaxation as follows inside poisson.C file as: Code:
fvScalarMatrix phiEqn
(
fvm::laplacian(phi) - beta * sinh(phi)
// fvm::laplacian(phi) - beta * (phi + (1/6)*pow(phi,3) + (1/120)*pow(phi,5) + (1/362880)*pow(phi,9) + (1/39916800)*pow(phi,11))
);
phiEqn.relax();
phiEqn.solve();
Now, the code runs for  , however, for , however, for  gives the same error: gives the same error:Code:
Iteration = 0.0005 DICPCG: Solving for phi, Initial residual = 1, Final residual = 7.04378610773e-12, No Iterations 79 ExecutionTime = 0.07 s ClockTime = 1 s Iteration = 0.00055 #0 Foam::error::printStack(Foam::Ostream&) at ??:? #1 Foam::sigFpe::sigHandler(int) at ??:? #2 in "/lib/x86_64-linux-gnu/libc.so.6" #3 __sinh_finite in "/lib/x86_64-linux-gnu/libm.so.6" #4 sinh in "/lib/x86_64-linux-gnu/libm.so.6" #5 Foam::sinh(Foam::Field<double>&, Foam::UList<double> const&) at ??:? #6 at ??:? #7 at ??:? #8 __libc_start_main in "/lib/x86_64-linux-gnu/libc.so.6" #9 at ??:? Floating point exception (core dumped) I will test the code with time derivative as well and produce the feedback.  Regards |
|
|
|

|
|
|
|
|
#20 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
I am not sure if my assumptions were correct. It was just a guess. Well, do you have the necessary entries in the fvSolutions? I think so, or not?
Code:
relaxationFactors
{
equations
{
phi 0.3;
phiFinal 1;
}
}
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| what is swap4foam ?? | AB08 | OpenFOAM | 28 | February 2, 2016 02:22 |
| implicit - scalar product source term in momentum equation | vinch | OpenFOAM Running, Solving & CFD | 0 | October 28, 2014 15:57 |
| UDF for source term in momentum equation | Enrico | FLUENT | 9 | May 30, 2014 12:34 |
| [swak4Foam] Swak4FOAM 0.2.3 / OF2.2.x installation error | FerdiFuchs | OpenFOAM Community Contributions | 27 | April 16, 2014 16:14 |
| [swak4Foam] build problem swak4Foam OF 2.2.0 | mcathela | OpenFOAM Community Contributions | 14 | April 23, 2013 14:59 |