 |
|
|
[Sponsors] | |||||
Parcel position: where it is updated? (OpenFOAM 3.x) |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 |
|
Member
Chris Cloney
Join Date: Jun 2016
Location: Halifax, Canada
Posts: 62
Rep Power: 10  |
I haven't figured it out yet, but I made some more progress.
When I print to info in calcVelocity: Code:
template<class ParcelType>
template<class TrackData>
const Foam::vector Foam::KinematicParcel<ParcelType>::calcVelocity
(
TrackData& td,
const scalar dt,
const label cellI,
const scalar Re,
const scalar mu,
const scalar mass,
const vector& Su,
vector& dUTrans,
scalar& Spu
) const
{
typedef typename TrackData::cloudType cloudType;
typedef typename cloudType::parcelType parcelType;
typedef typename cloudType::forceType forceType;
const forceType& forces = td.cloud().forces();
// Momentum source due to particle forces
const parcelType& p = static_cast<const parcelType&>(*this);
const forceSuSp Fcp = forces.calcCoupled(p, dt, mass, Re, mu);
const forceSuSp Fncp = forces.calcNonCoupled(p, dt, mass, Re, mu);
const forceSuSp Feff = Fcp + Fncp;
const scalar massEff = forces.massEff(p, mass);
Info<< "Fcp = " << Fcp << endl;
Info<< "Fncp = " << Fncp << endl;
Info<< "massEff = " << massEff << endl;
// New particle velocity
//~~~~~~~~~~~~~~~~~~~~~~
// Update velocity - treat as 3-D
const vector abp = (Feff.Sp()*Uc_ + (Feff.Su() + Su))/massEff;
const scalar bp = Feff.Sp()/massEff;
Spu = dt*Feff.Sp();
IntegrationScheme<vector>::integrationResult Ures =
td.cloud().UIntegrator().integrate(U_, dt, abp, bp);
vector Unew = Ures.value();
// note: Feff.Sp() and Fc.Sp() must be the same
dUTrans += dt*(Feff.Sp()*(Ures.average() - Uc_) - Fcp.Su());
// Apply correction to velocity and dUTrans for reduced-D cases
const polyMesh& mesh = td.cloud().pMesh();
meshTools::constrainDirection(mesh, mesh.solutionD(), Unew);
meshTools::constrainDirection(mesh, mesh.solutionD(), dUTrans);
return Unew;
}
Code:
Solving 1-D cloud limestoneCloud1 Fcp = ((0 0 0) 1.953585e-09) Fncp = ((0 0 0) 0) massEff = 1.308996939e-12 Fcp = ((0 0 0) 1.953266393e-09) Fncp = ((0 0 0) 0) massEff = 1.308996939e-12 Fcp = ((0 0 0) 1.952948152e-09) Fncp = ((0 0 0) 0) massEff = 1.308996939e-12 Fcp = ((0 0 0) 1.952630597e-09) Fncp = ((0 0 0) 0) massEff = 1.308996939e-12 My analytical equation in ptython is Code:
if Re > 1000:
Cd = 0.424
else:
Cd = 24*(1.0 + (1.0/6.0)*pow(Re,2.0/3.0))
dV = Vinf-V
Fd = 0.5*Cd*rhof*dV*dV*Ac
Fnet = Fd
A = Fnet/mp
V = V + 0.5*(A+Aold)*dt
Code:
template<class CloudType>
Foam::forceSuSp Foam::SphereDragForce<CloudType>::calcCoupled
(
const typename CloudType::parcelType& p,
const scalar dt,
const scalar mass,
const scalar Re,
const scalar muc
) const
{
forceSuSp value(vector::zero, 0.0);
value.Sp() = mass*0.75*muc*CdRe(Re)/(p.rho()*sqr(p.d()));
return value;
}
template<class CloudType>
Foam::scalar Foam::SphereDragForce<CloudType>::CdRe(const scalar Re) const
{
if (Re > 1000.0)
{
return 0.424*Re;
}
else
{
return 24.0*(1.0 + 1.0/6.0*pow(Re, 2.0/3.0));
}
}
Also, can anyone explain how the integrator works? I tried looking before but could not figure it out. Why are both abp and bp passed into it? This seems common across a lot of lagrange models. Code:
IntegrationScheme<vector>::integrationResult Ures =
td.cloud().UIntegrator().integrate(U_, dt, abp, bp);
|
|
|
|

|
|
|
|
|
#22 |
|
Member
Chris Cloney
Join Date: Jun 2016
Location: Halifax, Canada
Posts: 62
Rep Power: 10  |
Ok, I figured some more things out although I am stuck at a basic part.
The integrator has two models, an analytic one and Euler implicit one. I will reference the analytic one for now which solves the equation  Code:
template<class Type>
typename Foam::IntegrationScheme<Type>::integrationResult
Foam::Analytical<Type>::integrate
(
const Type& phi,
const scalar dt,
const Type& alphaBeta,
const scalar beta
) const
{
typename IntegrationScheme<Type>::integrationResult retValue;
const scalar expTerm = exp(min(50, -beta*dt));
if (beta > ROOTVSMALL)
{
const Type alpha = alphaBeta/beta;
retValue.average() = alpha + (phi - alpha)*(1 - expTerm)/(beta*dt);
retValue.value() = alpha + (phi - alpha)*expTerm;
}
else
{
retValue.average() = phi;
retValue.value() = phi;
}
return retValue;
}
   Therefore, the integrator solves:  So 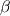 is the relaxation timescale between the fluid and particle velocity. Using the sphereDrag this value is then: is the relaxation timescale between the fluid and particle velocity. Using the sphereDrag this value is then: I have two questions that I cannot figure out from here. One, why isn't the integrator solving the following equation? It seems like this makes more sense than the other version.  and two, how is the relaxation timescale relation derived? I know I have done it before, but I cannot seem to figure it out. I found that fluent is solving the same equation (https://www.sharcnet.ca/Software/Flu...ug/node809.htm) but I do not understand why it includes CdRe/24. Shouldn't it just be Cd? I know it has something to do with stokes law, but cannot figure it out yet. Does anyone have a hint or reference? Thanks! |
|
|
|

|
|
|
|
|
#23 |
|
New Member
Timo Niemi
Join Date: Jun 2015
Posts: 5
Rep Power: 11  |
The integrator solves
 because it is the "analytic" solution of the particle velocity (assuming V_cell and Sp are constant during the time step, not true unless dt is small). As a thought experiment, consider two border cases: 1. dt = 0 -> no update to velocity 2. dt = infinity -> particle should approach cell velocity In case 1. the exp term is 1, giving  ie. the particle velocity stays the same. In case 2. the exp term goes to zero giving  ie. the particle velocity is the cell velocity. With  the results would not be logical. Hope this helps. |
|
|
|

|
|
|
|
|
#24 |
|
Member
Chris Cloney
Join Date: Jun 2016
Location: Halifax, Canada
Posts: 62
Rep Power: 10  |
Thanks Tniemi, that makes sense. I was thinking about it the wrong way.
I am still looking for a good reference on how the relaxation timescale is derived. I thought I remembered seeing it in the "Fundamentals of Multiphase Flow" textbook but could not find it in there. BTW, I figured out why my analytical solution from before was wrong. In addition to using the relaxation timescale equation instead of Fd = 0.5*rhof*A*dV^2, my Reynolds number calculation was wrong. It needs to be based on slip velocity not particle velocity. The updated plot looks like this Velocity_DragOnlyUpdated.jpg I am not sure why the particle skips around a bit reaching the maximum. The particles have coupled = false. The fluid velocity does fluctuate a bit, but only in the forth decimal place (e.g., 0.99917-1.0003) so I am not sure why the particle velocity is affected so much. Thoughts? |
|
|
|

|
|
|
|
|
#25 |
|
Member
Chris Cloney
Join Date: Jun 2016
Location: Halifax, Canada
Posts: 62
Rep Power: 10  |
I have moved on to multiphase laminar flame simulations for the time being and have ran into a problem with the trackToFace function in kinematicParcel::move(). I instrumented the function with print statements. The code and example output are shown in the next two windows.
Code:
template<class ParcelType>
template<class TrackData>
bool Foam::KinematicParcel<ParcelType>::move
(
TrackData& td,
const scalar trackTime
)
{
typename TrackData::cloudType::parcelType& p =
static_cast<typename TrackData::cloudType::parcelType&>(*this);
Info << "Starting particle move function" << endl;
td.switchProcessor = false;
td.keepParticle = true;
const polyMesh& mesh = td.cloud().pMesh();
const polyBoundaryMesh& pbMesh = mesh.boundaryMesh();
const scalarField& cellLengthScale = td.cloud().cellLengthScale();
const scalar maxCo = td.cloud().solution().maxCo();
scalar tEnd = (1.0 - p.stepFraction())*trackTime;
scalar dtMax = trackTime;
if (td.cloud().solution().transient())
{
dtMax *= maxCo;
}
bool tracking = true;
label nTrackingStalled = 0;
Info << " dtMax: " << dtMax << endl;
Info << " End Time: " << tEnd << endl;
Info << "Starting particle move loop" << endl;
int loopIndex = 0;
while (td.keepParticle && !td.switchProcessor && tEnd > ROOTVSMALL)
{
loopIndex++;
Info << " Loop index: " << loopIndex << endl;
Info << " End time: " << tEnd << endl;
Info << " Number stalled: " << nTrackingStalled << endl;
Info << " Position before correction: " << p.position() << endl;
// Apply correction to position for reduced-D cases
meshTools::constrainToMeshCentre(mesh, p.position());
Info << " Position after correction: " << p.position() << endl;
const point start(p.position());
Info << " Starting move Calculation: " << endl;
// Set the Lagrangian time-step
scalar dt = min(dtMax, tEnd);
Info << " dt: " << dt << endl;
// Cache the parcel current cell as this will change if a face is hit
const label cellI = p.cell();
const scalar magU = mag(U_);
Info << " Velocity Vec: " << U_ << endl;
Info << " Velocity Mag: " << magU << endl;
if (p.active() && tracking && (magU > ROOTVSMALL))
{
const scalar d = dt*magU;
Info << " Distance d: " << d << endl;
const scalar dCorr = min(d, maxCo*cellLengthScale[cellI]);
Info << " Distance dCorr: " << dCorr << endl;
Info << " Original position: " << p.position() << endl;
Info << " Hypothetical position: " << p.position() + dCorr*U_/magU << endl;
dt *=
dCorr/d
*p.trackToFace(p.position() + dCorr*U_/magU, td);
Info << " Final position: " << p.position() << endl;
Info << " dt_adjusted: " << dt << endl;
}
tEnd -= dt;
scalar newStepFraction = 1.0 - tEnd/trackTime;
if (tracking)
{
if
(
mag(p.stepFraction() - newStepFraction)
< particle::minStepFractionTol
)
{
nTrackingStalled++;
if (nTrackingStalled > maxTrackAttempts)
{
tracking = false;
}
}
else
{
nTrackingStalled = 0;
}
}
p.stepFraction() = newStepFraction;
bool calcParcel = true;
if (!tracking && td.cloud().solution().steadyState())
{
calcParcel = false;
}
// Avoid problems with extremely small timesteps
if ((dt > ROOTVSMALL) && calcParcel)
{
// Update cell based properties
p.setCellValues(td, dt, cellI);
if (td.cloud().solution().cellValueSourceCorrection())
{
Info << " Perform momentum and thermal calculation: " << endl;
p.cellValueSourceCorrection(td, dt, cellI);
}
p.calc(td, dt, cellI);
}
if (p.onBoundary() && td.keepParticle)
{
if (isA<processorPolyPatch>(pbMesh[p.patch(p.face())]))
{
td.switchProcessor = true;
}
}
p.age() += dt;
td.cloud().functions().postMove(p, cellI, dt, start, td.keepParticle);
}
return td.keepParticle;
}
Code:
Solving 1-D cloud limestoneCloud1 Starting particle move function dtMax: 1.5e-06 End Time: 5e-06 Starting particle move loop Loop index: 1 End time: 5e-06 Number stalled: 0 Position before correction: (0.007449940411 0.0001178373267 0.0001178373267) Position after correction: (0.007449940411 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 1.5e-06 Velocity Vec: (-1.63496736 0 0) Velocity Mag: 1.63496736 Distance d: 2.45245104e-06 Distance dCorr: 2.45245104e-06 Original position: (0.007449940411 0.0001178373267 0.0001178373267) Hypothetical position: (0.00744748796 0.0001178373267 0.0001178373267) Final position: (0.007449940349 0.0001178370321 0.0001178376213) dt_adjusted: 0 Loop index: 2 End time: 5e-06 Number stalled: 1 Position before correction: (0.007449940349 0.0001178370321 0.0001178376213) Position after correction: (0.007449940349 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 1.5e-06 Velocity Vec: (-1.63496736 0 0) Velocity Mag: 1.63496736 Distance d: 2.45245104e-06 Distance dCorr: 2.45245104e-06 Original position: (0.007449940349 0.0001178373267 0.0001178373267) Hypothetical position: (0.007447487898 0.0001178373267 0.0001178373267) Final position: (0.007449940287 0.0001178376213 0.0001178370321) dt_adjusted: 0 Loop index: 3 End time: 5e-06 Number stalled: 2 Position before correction: (0.007449940287 0.0001178376213 0.0001178370321) Position after correction: (0.007449940287 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 1.5e-06 Velocity Vec: (-1.63496736 0 0) Velocity Mag: 1.63496736 Loop index: 4 End time: 3.5e-06 Number stalled: 2 Position before correction: (0.007449940287 0.0001178373267 0.0001178373267) Position after correction: (0.007449940287 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 1.5e-06 Velocity Vec: (-1.635266068 0 0) Velocity Mag: 1.635266068 Loop index: 5 End time: 2e-06 Number stalled: 2 Position before correction: (0.007449940287 0.0001178373267 0.0001178373267) Position after correction: (0.007449940287 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 1.5e-06 Velocity Vec: (-1.635562618 0 0) Velocity Mag: 1.635562618 Loop index: 6 End time: 5e-07 Number stalled: 2 Position before correction: (0.007449940287 0.0001178373267 0.0001178373267) Position after correction: (0.007449940287 0.0001178373267 0.0001178373267) Starting move Calculation: dt: 5e-07 Velocity Vec: (-1.635857025 0 0) Velocity Mag: 1.635857025 My mesh is 1D with 5e-5 m cells. The other cell dimension is 2.36e-4 by 2.36e-4 (needed so my multiphase concentration works out correctly). The parcel itself is near the middle of the domain, away from any walls. As you can see the timesteps and displacements are quite small, so I am not sure what the problem is. I started looking at trackToFace but it looks complicated. Is there anyway I can just bypass it (I have outflow boundaries and am not looking to do parallel for the time being). Thanks! |
|
|
|

|
|
|
|
|
#26 |
|
Member
Chris Cloney
Join Date: Jun 2016
Location: Halifax, Canada
Posts: 62
Rep Power: 10  |
I found a fix to my trackToFace problem in the following thread: Documentation of trackToFace subroutine
The routine needs a normalization step to work properly on very high resolution meshes (micrometric). The thread also gives the original reference for the routine if anyone needs it. |
|
|
|

|
|
|
|
|
#27 | |
|
New Member
Tolga Cakir
Join Date: Oct 2017
Posts: 1
Rep Power: 0  |
Quote:
So start with particle assuming only a drag force acting on it, then Newton's second law is:  In this m_p represents the particle mass, which is volume of a sphere times density of particle, V_p is particle velocity and V is surrounding velocity and A is reference area which is the area of a circle in this case. Now divide left and right by the mass, so what we are left with is the expression for the drag force per unit mass:  Now we rewrite the right hand side slightly by multiplying and dividing by viscosity and diameter:  Now looking at the definition of Sp we see that it is defined as the force per unit velocity, because in the files for Sp and Su it says F=Sp(U-Up)+Su. So if we factour out  and again multiply by the particle velocity we have obtained the exact same expression as the one in the code. and again multiply by the particle velocity we have obtained the exact same expression as the one in the code.I hope this helps to understand where it comes from. |
||
|
|

|
||
|
|
|
#28 |
|
New Member
Arne Lampmann
Join Date: Feb 2018
Posts: 2
Rep Power: 0  |
Quote:
However, I struggle with the continuous flow velocity, which seems not to be taken into account in OF. When I have a look at the implementation of the Particle-Reynolds Number there is no Uc_ Code:
// Reynolds number
const scalar Re = this->Re(U_, d_, rhoc_, muc_);
|
|
|
|

|
|
|
|
|
#29 |
|
New Member
Arne Lampmann
Join Date: Feb 2018
Posts: 2
Rep Power: 0  |
Just had a look at the definition of the Reynolds number function in OF and everything is fine and accordingly to the derivation:
Code:
template<class ParcelType>
inline Foam::scalar Foam::KinematicParcel<ParcelType>::Re
(
const vector& U,
const scalar d,
const scalar rhoc,
const scalar muc
) const
{
return rhoc*mag(U - Uc_)*d/(muc + ROOTVSMALL);
}
|
|
|
|

|
|
 |
| Tags |
| kinematic cloud, parcel, positions |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Postdoc position available on hybrid CFD/Molecular-Dynamics using OpenFOAM | jasonreese | OpenFOAM | 0 | October 13, 2009 18:19 |
| DPM UDF particle position using the macro P_POS(p)[i] | dm2747 | FLUENT | 0 | April 17, 2009 02:29 |
| Postdoctoral position using OpenFOAM | schmidt_d | OpenFOAM | 1 | February 24, 2009 05:01 |
| Adventure of fisrst openfoam installation on Ubuntu 710 | jussi | OpenFOAM Installation | 0 | April 24, 2008 15:25 |
| Combustion Convergence problems | Art Stretton | Phoenics | 5 | April 2, 2002 06:59 |