[Kosdalak]

Hello,

I'm using some RAS models for the same case. After simulating a few 1000 iterations I want to compare the results of these models.

One of the things I want to compare is the Tensor R. With the command "postProcess -func R" it's possible to calculate the Reynolds Stress for the saved time steps. That works no worries so far.

But my question now is, HOW calculates OF this tensor exactly?

Does it just use the nut from each model and calculates it with the following equation or are there other "special" ways?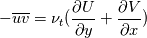





I want to compare four RAS models. The kEpsilon, komegaSST, v2f and the LienCubic. With "special" I mean for example that the LienCubic handles the 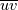diffrent than the other models.

I appriciate all kinds of help or hints!

Thanks in advance and Greetings
Jan

[Andrea1984]

Hi Jan,

The postProcess framework in OpenFOAM makes use of functionObjects. The "R" option will give you the field returned by the "R" method of the turbulence model that is in use in your case. In fact, I am guessing that the simple command

postProcess -func R

won't work, because R needs a turbulence model to be evaluated. Hence you have to execute (assuming that your solver is simpleFoam):

simpleFoam -postProcess -func R

This will instantiate the turbulenceModel object that you need. The field that will be created by

-postProcess -func R

is the volSymmTensorField returned by the R() method of that turbulenceModel object that is instantiated when you execute your solver.

You can see this in the implementation of the turbulenceFields functionObject in /src/functionObjects/field/turbulenceFields. So the way in which R is calculated in OpenFOAM depends on the turbulence model that you are using in your case.

For linear eddy-viscosity models this is:

template<class BasicTurbulenceModel>
Foam::tmp<Foam::volSymmTensorField>
Foam::eddyViscosity<BasicTurbulenceModel>::R() const
{
    tmp<volScalarField> tk(k());

    // Get list of patchField type names from k
    wordList patchFieldTypes(tk().boundaryField().types());

    // For k patchField types which do not have an equivalent for symmTensor
    // set to calculated
    forAll(patchFieldTypes, i)
    {
        if
        (
           !fvPatchField<symmTensor>::patchConstructorTablePtr_
                ->found(patchFieldTypes[i])
        )
        {
            patchFieldTypes[i] = calculatedFvPatchField<symmTensor>::typeName;
        }
    }

    return volSymmTensorField::New
    (
        IOobject::groupName("R", this->alphaRhoPhi_.group()),
        ((2.0/3.0)*I)*tk() - (nut_)*dev(twoSymm(fvc::grad(this->U_))),
        patchFieldTypes
    );
}

For non-linear eddy viscosity models, this is:

template<class BasicTurbulenceModel>
Foam::tmp<Foam::volSymmTensorField>
Foam::nonlinearEddyViscosity<BasicTurbulenceModel>::R() const
{
    tmp<volSymmTensorField> tR
    (
        eddyViscosity<BasicTurbulenceModel>::R()
    );
    tR.ref() += nonlinearStress_;
    return tR;
}

where you can see that there is a contribution due to non-linearity of the model. The nonlinearStress term is evaluated according to the specific non-linear eddy viscosity model that you use. For the Lien cubic kEpsilon this is:

void LienCubicKE::correctNonlinearStress(const volTensorField& gradU)
{
    volSymmTensorField S(symm(gradU));
    volTensorField W(skew(gradU));

    volScalarField sBar((k_/epsilon_)*sqrt(2.0)*mag(S));
    volScalarField wBar((k_/epsilon_)*sqrt(2.0)*mag(W));

    volScalarField Cmu((2.0/3.0)/(Cmu1_ + sBar + Cmu2_*wBar));
    volScalarField fMu(this->fMu());

    nut_ = Cmu*fMu*sqr(k_)/epsilon_;
    nut_.correctBoundaryConditions();

    nonlinearStress_ =
        fMu*k_
       *(
            // Quadratic terms
            sqr(k_/epsilon_)/(Cbeta_ + pow3(sBar))
           *(
                Cbeta1_*dev(innerSqr(S))
              + Cbeta2_*twoSymm(S&W)
              + Cbeta3_*dev(symm(W&W))
            )

            // Cubic terms
          - pow3(Cmu*k_/epsilon_)
           *(
                (Cgamma1_*magSqr(S) - Cgamma2_*magSqr(W))*S
              + Cgamma4_*twoSymm((innerSqr(S)&W))
            )
        );
}

Hope this clarifies it.
Andrea

[Kosdalak]

Hi Andrea,

Thank you very much! That was exactly what I needed to know.
I'm using piso, but it works the same - that I know.



So it is really dependet on which model I use. OF suprises me everytime


For the linear eddy-viscosity models, the code means mathematically the following right?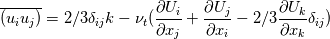





I'm still a bit confused about the last term because in the Boussinesq assumption it does not appear. Or where am I failing?

Again, thank you for the detailed answer.

Greetings

Jan

[Andrea1984]

No worries, glad it helped.

Yes, the equation is the standard expression that you reported for linear eddy-viscosity models for the deviatoric part of the Reynolds Stress tensor.

The term

\frac{2}{3} \frac{\partial U_k}{\partial x_k} \delta_{ij}

is equal to zero for constant-density flows, so you probably should not worry about it.

Andrea

[Kosdalak]

Oh yeah, I was not thinking so far.

Thanks again!

Greetings
Jan