 |
|
|
[Sponsors] | |||||
Mathematical meaning of window averaging in fieldAverage functionObject |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
I have been taking a look at the fieldAverage functionObject, for time averaging fields during a simulation. The basic implementation is cunningly coded to use the minimum amount of storage, by calculating the mean and variance at the new time step using the latest data and the mean from the old time step. You can show through some simple algebra that this provides an exact estimation of the mean and variance, based on the complete sample set.
Now, my question is, what do you get when you use the "window" function? In an ideal world, for a window size of w samples, it would be the average over the last w samples, but this is clearly impossible to calculate without storing w samples, since you can't simply discard the (n-w)'th sample. But does the window function give something that approximates this? Let's take a look. The algorithm for the mean value of 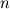 samples (see fieldAverageTemplates.C) is: samples (see fieldAverageTemplates.C) is:  , where , where  (assuming no windowing and equal spaced samples) and (assuming no windowing and equal spaced samples) and  is the average of the first is the average of the first  samples. Expanding out samples. Expanding out  , you can show that this reduces to , you can show that this reduces to  , as desired. , as desired.Now, if windowing is active with a window size of  , then when the number of samples exceeds the window size the following limit is applied: , then when the number of samples exceeds the window size the following limit is applied:  , where , where 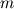 is now a constant. Let's take an example with a window size of 2 samples ( is now a constant. Let's take an example with a window size of 2 samples ( here): here):     etc. - you can see the pattern. My question is - what the heck is this quantity? It clearly slowly diminuishes the effect of the earlier samples, but the average is slightly biased to the most recent samples (that's exaggerated in the above example; for larger values of m, then  and the biasing is less strong). It's certainly not a balanced average of the recent and the biasing is less strong). It's certainly not a balanced average of the recent  samples. samples. So what is the physical meaning of the windowed average, and when might you want to use it? |
|
|
|

|
|
|
|
|
#2 |
|
New Member
navid toussi
Join Date: Nov 2015
Posts: 20
Rep Power: 11  |
Very good thread! Have you got the answer? If so, would you mind sharing it here? Thanks
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
Given the silence from the community on this one, I think it's safe to assume that there probably is no clear meaning to the quantity and I'm not sure why/when you would ever want to use it.
Here's my interpretation of the quantity: start off with the initial definition:  and rearrange:  and now you see that the change in the average value is the weighted difference between the new instantaneous value and the old mean, with the weight being  . . This can be visualised in the following chart, for a sequence of n=20 and window values of m = 2, 5 and 10. The chart shows the factors on the  values in the arithmetic sequence (refer back to my original post) ... as can be seen, there's no real meaning to the result - it's not an average of the last m values, which was what I originally thought it might be aiming to provide. It's just a complex mash of all of the previous values, with higher weighting to the more recent values. values in the arithmetic sequence (refer back to my original post) ... as can be seen, there's no real meaning to the result - it's not an average of the last m values, which was what I originally thought it might be aiming to provide. It's just a complex mash of all of the previous values, with higher weighting to the more recent values.So, all in all - unless someone can provide a justification, my advice is to ignore it. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Time averaging of new variable using fieldAverage | Mirage | OpenFOAM Post-Processing | 6 | November 9, 2019 22:30 |
| Averaging a field created by a functionObject | me3840 | OpenFOAM Post-Processing | 2 | October 3, 2018 12:58 |
| fieldAverage - window and periodicRestart | mechkween | OpenFOAM | 1 | April 17, 2018 04:19 |
| fieldAverage fails to continue averaging the fields | FernandoSoares | OpenFOAM Programming & Development | 6 | December 8, 2015 16:43 |
| Starting field averaging using libFunctionObject after certain time | eelcovv | OpenFOAM Programming & Development | 25 | December 7, 2015 23:28 |