 |
|
|
[Sponsors] | |||||
Mapping bulk temperature of channel and moutend cylinder flow cases into field |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Jan 2019
Posts: 2
Rep Power: 0  |
Hi fellow foamers,
Problem description: I'm trying to represent the non-dimensional temperature 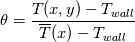 , ,throughout a 2D channel in Paraview, in which 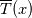 is the bulk temperature for the transverse surface positioned in the is the bulk temperature for the transverse surface positioned in the  longitudinal coordinate. longitudinal coordinate. 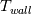 in the present case is constant. in the present case is constant.The bulk temperature for a section,  , in a given longitudinal coordinate is given by , in a given longitudinal coordinate is given by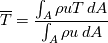 , ,where 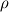 is the fluid density and is the fluid density and  the velocity component normal to section the velocity component normal to section 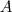 . .Achievements so far: So far I've been using swak4foam's funkyDoCalc coupled with a bash script to cycle through the longitudinal coordinate in order to create an array of the bulk temperature along the channel. The swak4foam script: Code:
s1
{
type swakExpression;
valueType surface;
verbose true;
expression "sum(T*rho*Sf()&U)/sum(rho*Sf()&U)";
accumulations (
average
);
surfaceName x1;
surface {
type plane;
source cells;
surfaceTupe searchablePlate;
planeType pointAndNormal;
pointAndNormalDict {
basePoint (0 1e-6 1e-6);//the bash script uses sed to change the x coordinate of the basepoint
normalVector (1 0 0);
interpolate true;
}
}
}
Up to this point I have an array of the bulk temperature throughout the longitudinal coordinate. Current obstacle/issue: I want to map this bulk temperature array to a scalar field, in which 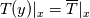 , i.e., for a given longitudinal position, , i.e., for a given longitudinal position,  , the transverse temperature is set to the correspondent bulk temperature for any transverse position. , the transverse temperature is set to the correspondent bulk temperature for any transverse position.After obtaining this bulk temperature field I could then use the Calculator function in Paraview to determine the non-dimensional temperature field 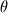 . .All help is welcomed. Thank you. |
|
|
|

|
|
 |
|
|