 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Nereus
Join Date: Sep 2011
Posts: 18
Rep Power: 15  |
Hi:
I have a question about finite volume methods, specifically regarding the calculation of fluxes at control volume faces. The books I have read devote a lot of time to discuss the reconstruction of scalar variable 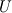 at these faces. For example, the reconstruction of at these faces. For example, the reconstruction of 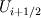 . Then, it is usually stated that we can calculate the flux, . Then, it is usually stated that we can calculate the flux, 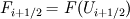 , and everything is peachy. I understand the reconstruction of , and everything is peachy. I understand the reconstruction of 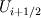 , but what confuses me is if, for instance, I'm considering an advective flux, what velocity do I use with the reconstructed variable at , but what confuses me is if, for instance, I'm considering an advective flux, what velocity do I use with the reconstructed variable at 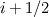 to get my flux? A simple average velocity at the control face? to get my flux? A simple average velocity at the control face?In short, do I also have to go through the reconstruction process that I used for the scalar variable for the velocity vector? |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Nereus
Join Date: Sep 2011
Posts: 18
Rep Power: 15  |
I suppose all I'm really asking is, if I know the velocity field at the nodes how do I interpolate to achieve velocities at control volume faces (using a median-dual scheme)?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
duri
Join Date: May 2010
Posts: 245
Rep Power: 17  |
I suppose U is conservative/primitive variable. Once you got it for all equation it is easy to estimate variables needed at face.
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Nereus
Join Date: Sep 2011
Posts: 18
Rep Power: 15  |
But, how? Say, for example, U is some tracer concentration and I know the velocity field at all nodes. How do I then determine the velocity field at the face of the control volume? As I say, there's a lot of literature on reconstructing U (i.e., scalar conservative variables), but no word on the velocity field.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
duri
Join Date: May 2010
Posts: 245
Rep Power: 17  |
When you are solving let say 2D Euler, reconstruct r,ru,rv (r-density) at the face like a scalar variable. Once you got this you can get u and v at face by ru/r and rv/r. Its straight forward.
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
Nereus
Join Date: Sep 2011
Posts: 18
Rep Power: 15  |
Thanks for the replies, duri. I'm not actually solving CFD (i.e., Euler or Navier-Stokes) equations, but just general conservation law equations using finite volume methods. So, I prescribe a velocity field onto the grid, I just don't know the best way to interpolate this field to my control volume faces. Would simple linear interpolation along edges work? Or do standard methods like MUSCL work for vectors like velocity fields, too? I realise that this may seem like a trivial point to those in the know, but I'm at a loss to figure out the best way to achieve this.
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Aug 2011
Posts: 272
Rep Power: 16  |
Hi Nereus,
Let's imagine you want to solve a transport equation for a scalar phi. This variable is convected by U velocity. When integrating over a control volume the convection term div(Uphi) where div is the divergence operator you will have to express U and phi on all control volume faces. let's say at i+1/2. Generally U at i+1/2 is expressed using a simple interpolation function. For example if your grid is regular you could use Ue=(UP+UE)/2 "e" stands for the location i+1/2 For phi variable you have to choose a discretization scheme. There exist a tons of such schemes (CDS, UDS, Hybrid, Power-Law, TVD schemes, ENO, WENO , blended schemes....) there are really a big choice according the type of your transport equation (dominated convection equation, Hyperbolic equation,...) You have to distinguish the scheme used for phi and the one for U. If phi=U then you may have two different schemes. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
answering to your question depends on what you are solving, compressible or incompressible flows... in the first case I suggest the book of LeVeque on FV method for hyperbolic systems, in the second case the book of Ferziger and Peric is useful for addressing the flux interpolation issue.
Do not forget that the colocation of the variables can be staggered or non-staggered. |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Nereus
Join Date: Sep 2011
Posts: 18
Rep Power: 15  |
Thanks, leflix, that's exactly what I was after. I reconstruct my scalar variable using Barth & Jespersen's linear piecewise reconstruction and calculate the flux using Kurganov & Tadmor's scheme, I just needed to know what the velocity was at the faces. I'll use a simple interpolation, as you suggest.
Thanks for the reply, Filippo. I'm not solving a fluids problem as such, but rather a general conservation equation. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
if you are involved only on a formal reconstruction problem for conservation laws, perhaps you can do best by using spectral polynomials
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] mesh airfoil NACA0012 | anand_30 | OpenFOAM Meshing & Mesh Conversion | 13 | March 7, 2022 18:22 |
| Finite Difference Vs. Finite Volume | elankov | Main CFD Forum | 43 | December 18, 2010 17:30 |
| Finite Volume WENO Scheme | DSS | Main CFD Forum | 3 | January 15, 2007 04:47 |
| Finite volume or finite differene for free surface | G N Xie | Main CFD Forum | 8 | January 10, 2005 08:42 |
| Unstructured grid finite volume methods | Marcus | Main CFD Forum | 3 | December 5, 2000 01:25 |