 |
|
|
[Sponsors] | |||||
finite element method for the Shallow Water Equations help |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
John Smith
Join Date: Dec 2011
Posts: 4
Rep Power: 15  |
Hello,
I try to solve the Shallow Water Equations using finite element methods. Can anyone explain me how to treat nonlinear terms? The problem is that we can write linear terms as matrix-vector multiplication where matrix is independent on time. For example for the height field h we have  after getting the Galerkin equation by multiplying on test function and integrating over domain we will get the term like 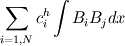 or in the matrix form  Hence we compute the matrix only once and then multiply by updated coefficient vector But how to deal with the terms like $uh$? where u is the velocity  after getting the Galerkin equation this will be like  How these can be represented in the matrix form in order not to compute all these integrals on each timestep? Last edited by alvesker; December 4, 2011 at 22:54. Reason: typo |
|
|
|

|
|
|
|
|
#2 |
|
Member
|
Dear alvesker,
you don't have to write the FEM approximated form of each parameter 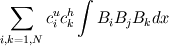 is more accurate, though, I would suggest writing the the mean value of those parameters to simplify the weak form. is more accurate, though, I would suggest writing the the mean value of those parameters to simplify the weak form.about the integration on each time step it depends on the grid form you are using to split the domain. Last edited by seyedashraf; December 5, 2011 at 05:52. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
John Smith
Join Date: Dec 2011
Posts: 4
Rep Power: 15  |
Dear seyedashraf,
Thanks for the quick reply. Can you explain what do you understand by the mean value? is it like the following?  and how write it to the terms like  where u, h are the velocity component and height field  So if apply the FEM we have  what is the average in the case when in the multiplication one of unknows one contain gradient (we have these in the advection formulation) Last edited by alvesker; December 6, 2011 at 00:20. Reason: add |
|
|
|

|
|
|
|
|
#4 |
|
New Member
John Smith
Join Date: Dec 2011
Posts: 4
Rep Power: 15  |
the grid form - I use triangular grid
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| What is C.V. based finite element method | C-H Kuo | Main CFD Forum | 4 | September 19, 2022 15:06 |
| Lattice Boltzmann method vs Finite Element Method and Finite Volume Method | solemnpriest | Main CFD Forum | 3 | August 12, 2013 12:00 |
| OpenFOAM-extend, Finite Element Method (FEM) | Martin80 | OpenFOAM Programming & Development | 1 | December 3, 2011 07:28 |
| finite element method | harten | Main CFD Forum | 0 | November 1, 2007 06:37 |
| BCs of hyperbolic Shallow Water Equation | Kang, S. K. | Main CFD Forum | 4 | November 21, 2000 22:20 |