November 30, 2011, 16:11
|
Green's theorem or divergence theorem?
|
#1
|
|
New Member
Join Date: Jul 2010
Posts: 10
Rep Power: 16
|
Hi,
I want to calculate the total flux but I'm not sure if I have to use Green's theorem (2D) or the divergence theorem (3D). The equation below is a modified Reynolds equation describing the air flow in the clearance of porous air bearing.
P is the pressure in the clearance of the air bearing, P' is the pressure in the porous media. However, at Z=1 P' must be equal to P for continuity.
This equation can be rewritten using the divergence vector operation:
![\nabla\bullet\left[PH^3 \frac{\partial P}{\partial\theta} + (\frac{R}{L})^2 PH^3 \frac{\partial P}{\partial Y} - \Lambda PH + \Psi P P'\right] = 0](/Forums/vbLatex/img/3f4f43896a15af283806de574d743a33-1.gif "\nabla\bullet\left[PH^3 \frac{\partial P}{\partial\theta} + (\frac{R}{L})^2 PH^3 \frac{\partial P}{\partial Y} - \Lambda PH + \Psi P P'\right] = 0")
Solving this equation with a numerical method (i.e. finite difference) can be done by first simplifying the equation with Green's theorem for flux or the divergence theorem. Because I'm interested in the flow in the 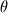 - Y direction I want to solve the equation applying Green's theorem (2D). However, in the first equation there is also a gradient in the Z-direction namely  . So my question is: Can I calculate the flux with Green's theorem or do I have to use the divergence theorem because of the pressure gradient in the Z-direction?
|
|
|
Similar Threads
Linear Mode
