 |
|
|
[Sponsors] | |||||
Linearization of viscous flux in discontinuous Galerkin finite element methods |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Yidong
Join Date: Nov 2011
Posts: 23
Rep Power: 15  |
I'm a student studying discontinuous Galerkin (DG) finite element methods in CFD.
Many papers related to implicit DG methods for Navier-Stokes equations claim that the linearization of viscous flux (viscous Jacobian matrix) is computed analytically, but provide no more details. In finite volume methods, it's not necessary to compute the viscous Jacobian matrix explicitly. A common simplification is to use the spectral radius instead of analytically derived viscous Jacobian matrix. However for DG methods, I haven't seen any papers addressing the derivation of viscous Jacobians explicitly. So far as my own experience can tell, if the linearization of viscous flux is not treated carefully, the implicit solver will not work.  If it happens that you are familiar with DG methods, I'll appreciate so much if you would share your experience and discuss with me  
|
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
|
If you treat any coefficients in the viscous terms as constants, then the viscous terms are linear, e.g.,
 , consider , consider 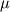 to be constant for derivation of implicit scheme. Assembling such terms will give you A*U where A is a matrix and U is the vector of unknown solution. The linearization of this is just A*dU. At the analytical level, you have a bilinear for a(u,v) representing the viscous terms. Its linearlization is just a(du, v) whose assembled version is A*dU. to be constant for derivation of implicit scheme. Assembling such terms will give you A*U where A is a matrix and U is the vector of unknown solution. The linearization of this is just A*dU. At the analytical level, you have a bilinear for a(u,v) representing the viscous terms. Its linearlization is just a(du, v) whose assembled version is A*dU.
|
|
|
|

|
|
 |
| Tags |
| implicit method, navier stokes equations |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Finite Element vs Cartesian Grip methods | Sidi | Main CFD Forum | 0 | December 15, 2005 11:40 |
| comments on FDM, FEM, FVM, SM, SEM, DSEM, BEM | kenn | Main CFD Forum | 2 | July 18, 2004 19:28 |
| Finite Difference, Element & Volume methods | JonS | Main CFD Forum | 10 | July 18, 2004 06:35 |
| Discontinuous Galerkin finite element method | Tony | Main CFD Forum | 0 | May 27, 2003 19:48 |