[maximsch2]

I am implementing discontinuous galerkin code (based on book by Hesthaven& Warburton) for lattice boltzman method (essentially system of linear advection equations). I am using upwind (= Lax–Friedrichs) flux and triangular mesh to solve Lid-driven cavity problem. Judging from results, my simulation is killed by numerical viscosity - 'real' Re is lower than I set. Preliminary research shows, that it may be caused by upwind flux. Is it true? What other fluxes should I try?

PS: before moving to DG I've implemented finite volume method, and observed the same problem there - upwind flux was too dissipative, I had to use central flux. But as far as I understand, central flux is bad for problems with discontinuities, which I am planning to simulate, so I need another solution.

[gory]

Lax–Friedrichs is a very dissipative flux.
Try Roe's flux. Here is a f90 subroutine:
http://www.ossanworld.com/cfdbooks/c..._fluxes_v2.f90
which is known to be accurate enough for viscous simulations.

gory

[praveen]

DG is often used with lax-friedrichs flux with very good results for euler equations. The high spatial accuracy of DG means that dissipation terms are small in lax-friedrichs flux. What is the polynomial degree of your basis functions ? If you discuss your equations, and how you choose the dissipation coefficient in lax-friedrichs flux, maybe somebody can give better help.

[maximsch2]

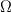My equation is: Where u is 2d vector, v is constant 2d vector. depends on u. Now I am using simple upwind flux: if n*u >= 0 I use value from current cell, if n*u < 0 I use value from neighbor. I am running my code with different polynomial degrees (from N=1,3,5) and observe similar behavior with all of them. I am trying to solve 2D lid-driven cavity problem, so I am approaching steady state by making a lot of time steps (~1M), for time stepping I now use 4th order Low-Storage Explicit Runge-Kutta.

[praveen]

You should first test that the scheme gives good answers for a pure convection equation, and compare with exact solutions. That will validate your DG scheme. The advection equations are supposed to model viscous solutions in some way since you mentioned lid-driven cavity flow problem. You need to study under what conditions they give a good approximation to NS solutions.

[maximsch2]

I guess DG code is OK, because I get some results for cavity flow. The problem is that in those results flow looks like Reynolds number is lower than I set.

[maximsch2]

Originally Posted by gory

Lax–Friedrichs is a very dissipative flux.
Try Roe's flux. Here is a f90 subroutine:
http://www.ossanworld.com/cfdbooks/c..._fluxes_v2.f90
which is known to be accurate enough for viscous simulations.

I've looked at Roe's flux, but it seems to me that in scalar linear case it is equal to upwind flux, isn't it?

[maximsch2]

Ok, I've investigated this problem a bit more and now I am completely confused.
I've read that Godunov flux is the least diffusive flux.
My code for Godunov flux:

def godunov_flux(left_val, right_val, ux, uy, nx,  ny):    
    un = nx*ux+ny*uy
    if left_val <= right_val:
        # min f(u)
        if un >= 0:
            return left_val
        else:
            return right_val
    else: # left_val > right_val
        # max f(u)
        if un >= 0:
            return left_val
        else:
            return right_val

Where ux, uy - components of speed from eqation. nx, ny - normals. left_val, right_val - values at the interface. Return value is multiplicated by un in the outer function, so it is not needed here. But looking at this function it looks exactly like upwind flux (=Lax–Friedrichs flux), which is supposed to be very dissipative....

[gory]

For a scalar advection equation, many schemes reduce to an identical scheme.
Godunov, Roe, Flux-vector-splitting, etc., all becomes the same upwind scheme.
BTW, this is my understanding of Lax-Firedrichs scheme:
http://en.wikipedia.org/wiki/Lax%E2%...edrichs_method

From your code, it looks like you have an upwind scheme.

[maximsch2]

That code was supposed to be for Godunov's exact Rieman solver:

Godunov(left_u, right_u):
   if left_u < right_u: return min(f(u))
   else: return max(f(u))

In case of scalar linear advection it just happens, that this solver is identical to upwind.
Lax-Friedrichs flux:
LF(left_val, right_val) = 0.5*(f(left_val) + f(right_val) - abs(un)*(right_val-left_val)) which is equal to 0.5*(un*(left_val + right_val) - abs(un)*(right_val-left_val)) = { un*left_val if un < 0 and un*right_val if un is > 0}
So Lax-Friedrichs flux is also identical to upwind flux.
This leaves me with choice of two fluxes: upwind and central. And central becomes unstable at some point while increasing Re, so I am stuck with upwind flux.
Is there any other flux that could be used for scalar linear advection, and which produces little numerical dissipation

[fuser]

Hi, some of the most involved researchers in the DG-LBM demonstrated good fluid flow data for the lid-driven cavity problem at high Re number; see, for example,

M. Min and T. Lee. A spectral-element discontinuous Galerkin lattice
Boltzmann method for nearly incompressible flows. J. Comput. Phys., 230, 245-259, 2011.

who implemented Lax-F. flux...

I have implemented the above method for a specific element type...and I obtain good results too at Re=5000, as demonstrated by comparing them with literature data. I suspect that your simulation is dominated by errors due to a high Mach number (what is yours? and Re?), and/ or your code does not have properly implemented one or more building blocks of the method (not the numerical flux).
Cheers

[maximsch2]

fuser, Thank you! Actually I've already found the problem - turned out it was in my code (wrong handling of one of the sides of triangles).

[fuser]

cool, I am glad you found the code error quickly.
Regards