 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
I have seen a number of forum posts on this topic but I'm still struggling with my boundary conditions.
I'm running a 1-D spherical calculation (only radial dependence considered). I decided to have velocity boundary conditions at the inlet and outlet. So the BCs I have are: inlet:  outlet:  which is zero gradient BC. which is zero gradient BC.I understand that for subsonic simulations you either have to specify velocity or pressure BCs. I have a staggered grid where the velocities are staggered forward. My discretised equation for the pressure looks of the form  I used the discretised equation to calculate the pressure values at the boundary. At the inlet since I have  therefore, I do not have therefore, I do not have  in the discretised pressure equation and for the outlet I do not have in the discretised pressure equation and for the outlet I do not have  . Is this correct? . Is this correct?
|
|
|
|

|
|
|
|
|
#2 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 16  |
How can you have 0 velocity in and non-zero velocity out, unless of course you are generating matter inside your volume?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
I'm studying combustion where the zero-upstream velocity is a far-field velocity and there is a flame in the middle of the domain and the boundary condition at the outlet is a zero-gradient boundary condition but the flow reaches about 60 m/s at this outlet.
I was at first baffled by your question but I think the combustion, creates density difference which creates mass. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 16  |
Could you maybe sketch your geometry?
I understood it as: Flame (r=0)-----inlet (r=r_i)-----------outlet (r=r_o)----> radial coordinate Please bear with me if that is not how it looked :-) |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
It's actually,
Outlet (r=0) ----------------------------------------Flame------------------Inet (r=R) I use a normalised temperature to define the flame location. I study spherical explosions where the flame starts at the centre and moves radially outward. Therefore at the centre (r=0) is the highest temperature (burnt side) where the normalised temperature C=1. I end simulations before the flame reaches R (end of the domain). Since there is no flame here, the normalised temperature C=0 at the outlet. So the profile of normalised temperature (C) looks like a backward ramp function. So the flame actually moves from left to right during my calculations. However, relative to the flame is the flow velocity, so for a particle fixed on the flame the flow direction will be from right-to-left. That's why I defined my inlet to be at r=R, and outlet to be at r=0. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 16  |
Ok, I think I get it finally. These are suggestions, I am by no means a CFD expert ...
With regards to the pressure: for symmetry you should have a zero gradient at r=0, so then P(N)=P(N-1), where N is the outlet node and N-1 is the node right next to it (here to the EAST). You could do that by setting  , ,  , ,  and and  in the pressure-equation written above. in the pressure-equation written above.At the inlet boundary (r=R), I would specify that the pressure on the EAST point would be equal to the ambient pressure P0. You could do by lumping  into the source term (b). In b, I think the velocities at the faces are also given, so there you would have to specify that the velocity at east face is 0. into the source term (b). In b, I think the velocities at the faces are also given, so there you would have to specify that the velocity at east face is 0.Let me hear what you think. Regards |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Hi thanks very much for the quick reply.
I'm still confused. This is a lengthy reply but I'm trying to understand certain things between what I have now and what you've just told me. So I'm using SIMPLER as I said before and I use a staggered grid. What I have now is a zero-gradient BC at the outlet (r=0) for velocity which says  . Am I correct in thinking that if I have this velocity BC then I can't have a pressure BC at the same location for incompressible flow? . Am I correct in thinking that if I have this velocity BC then I can't have a pressure BC at the same location for incompressible flow?At this boundary I discretise the pressure equation to obtain (just neglecting a_w term):  and according to SIMPLER method the mass source term b looks like  ------------- (1) ------------- (1)where r_P, r_w and r_e are the radii at the relevant points along the grid (these terms only come about because of the spherical discretisaiton). Also my grid is staggered and I store the velocities at the velocity-cell faces. So with my current boundary conditions I set  , where the pseduo-velocities are only calculated for the internal nodes. The problem with this is that the , where the pseduo-velocities are only calculated for the internal nodes. The problem with this is that the 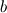 term doesn't go to zero at this location for spherical coordinates. This is ecause even though the velocities term doesn't go to zero at this location for spherical coordinates. This is ecause even though the velocities  and and  are the same, the change in radii are the same, the change in radii  and and  creates a source. So even if I have neglected the creates a source. So even if I have neglected the  in the discretised equation for this boundary in the discretised equation for this boundary  . Therefore, this violates symmetry. So am I right in thinking that rather than having zero-gradient with respect to velocity I should have zero-gradient with respect to pressure? . Therefore, this violates symmetry. So am I right in thinking that rather than having zero-gradient with respect to velocity I should have zero-gradient with respect to pressure?With regards to the inlet (r=R) BC, I have the discretised equation  by just neglecting a_E. A problem I have now is that I don't know what the cell face velocities should be at this location for a staggered grid to evaluate 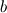 according to Eq.(1). At the end I do not have according to Eq.(1). At the end I do not have  since it's that point is outside the grid, but I set since it's that point is outside the grid, but I set  . However, my boundary condition for . However, my boundary condition for 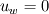 . So despite the fact that there is a radius change the mass term b goes to zero here since the velocities are zero anyway. I'm really not sure about this bit. . So despite the fact that there is a radius change the mass term b goes to zero here since the velocities are zero anyway. I'm really not sure about this bit.
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
Actually I realise that I don't include the centre point of the sphere, r=0 because it creates a singularity. Instead I start it at r=a, some finite value. So I'm not sure if I need to have symmetry BCs in this case.
|
|
|
|

|
|
|
|
|
#9 |
|
New Member
Tobias Elmøe
Join Date: Oct 2010
Location: Denmark
Posts: 9
Rep Power: 16  |
If your centre point for the pressure discretization is at 0, then wouldn't the control volume at that point would be a sphere, rather than a spherical shell? Then you only have flow out of there, right?. I think this should change your discretized equations there.
With regards to the inlet, you could move the grid for the pressure so it does not end at r=R, but at  . Then as you are staggering the velocity grid forward . Then as you are staggering the velocity grid forward  your last velocity node will be at r=R, right? In 'b' in the pressure-equation you could set u_e = 0, while keeping u_w from your solution to the momentum equation. Also you set a_E = 0 here, as you already wrote. your last velocity node will be at r=R, right? In 'b' in the pressure-equation you could set u_e = 0, while keeping u_w from your solution to the momentum equation. Also you set a_E = 0 here, as you already wrote.Again, I'm by no means sure of this.. I don't remember seeing an example in the textbooks I've been reading except for Patankar, regarding discretization in spherical coordinates and that wasn't for the NS equations). Hopefully someone more qualified will answer you soon 
|
|
|
|

|
|
|
|
|
#10 |
|
New Member
alex
Join Date: Oct 2010
Posts: 4
Rep Power: 16  |
Hello, I am a mechanical engineering.I need to use a subroutine ables to solve (in unsteady condition) 3-D fluid flow (the pressure and velocity and temperature) fields in cylindrical coordinate .Who Can send me the source code for SIMPLE / SIMPLER scheme (preferably on fortran) so that I can get & proceed from it.
please send me through my email, ahazbavi@ymail.com. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Impinging Jet Boundary Conditions | Anindya | Main CFD Forum | 25 | February 27, 2016 13:58 |
| [Gmsh] Import problem | ARC | OpenFOAM Meshing & Mesh Conversion | 0 | February 27, 2010 11:56 |
| Fluent accuracy and boundary conditions | Paolo Lampitella | FLUENT | 0 | June 12, 2008 07:25 |
| Pressure boundary conditions | Lionel S. | Main CFD Forum | 1 | August 24, 2007 19:03 |
| A problem about setting boundary conditions | lyang | Main CFD Forum | 0 | September 19, 1999 19:29 |