 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
|
Why are there some convection schemes only suitable for steady problems, while others can be used for both steady and unsteady problems? What are the core differences between these two classes schemes (for steady or unsteady problems)?
For example, Sweby's TVD scheme which is based on Lax-Wendroff and Warming-Beam schemes are not suitable for steady problem? why? Some one told me, "if there is no second order time-related artificial diffusion term and if the schemes itself only contains fourth order diffusion term, then it will be suitable for both steady and unsteady problems.” But I am not sure this is right and I can not understand, can any one help me? |
|
|
|

|
|
|
|
|
#2 |
|
Member
Join Date: Mar 2009
Posts: 32
Rep Power: 17  |
What do you mean by "suitable"?
To me, any schemes can be used for both steady and unsteady calculations. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
If you write, say, the lax wendroff scheme (even the non limited one) you will easily see that at the steady state, which is when u_i(n+1) = u_i(n), you will have a solution that is cfl dependent. The same is true for the Beam & Warming scheme (see Hirsch: Numerical Computation of Internal & External Flows).
This is because these schemes are derived as "one piece" time-space integration methods. The modern approach is to separately discretize space and time derivatives (a.k.a. method of lines). |
|
|
|

|
|
|
|
|
#4 |
|
Member
Join Date: Mar 2009
Posts: 32
Rep Power: 17  |
The solution is CFL dependent anyway whether it is steady or unsteady if the scheme has a disspation coeficient involving a time-step (LW or BW or Lax-Friedrichs, etc). For example, the solution produced by the Lax-Friedrichs scheme gets more dissipative for smaller CFL numbers. On the other hand, the dissipation coefficient of the first-order upwind scheme is independent of CFL; indeed the solution is insensitive to the CFL number for both steady and unsteady calculations. So, I still don't see why some scheme are "suitable" for steady calculations and others are not.
Again, I wonder what "suitable" means. |
|
|
|

|
|
|
|
|
#5 |
|
Member
|
About the "suitable" mean, I give an example, normally there are two simple methods to get bounded solution, one is based on TVD 'total-variation dimishing' while the other one based on CBC ' the convection -boundedness criterion',
TVD schmes are always used for unsteady problem, and CBC related schemes are used for steady problem. |
|
|
|

|
|
|
|
|
#6 |
|
Member
|
I know little about the line method.
I guess it means the spatial discretization and temporal integration are considered separately. And clearly the Lax-Wendroff scheme does not belong to this class. It combined time and space discretization. I think both of the two kinds of methods can be used to solve unsteady problems. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
|
As i said, this is not a "limiting" issue but comes from the way the equation is integrated in time. The "method of lines" just means that you integrate space and time derivative separately so that when the time derivative is zero the time step simply disappears.
In contrast, to properly integrate an unsteady problem you have to take in to account the unsteadyness in the limiting of the convective scheme, at least when considering the limiters in the Sweby diagram (TVD). In the case of the CBC, which is formulated in the NVD, if i remember well the 2nd order accuracy requirement is missing, that is the limiter should pass through the point (1/2,3/4), but this point is not excluded from the CBC region so you can actually realize a limiter which satisfy the CBC and preserves 2nd order accuracy. For example, Fluent uses a Bounded Central Scheme (with a form of the gamma limiter described by Jasak) which is second order accurate for smooth flows. |
|
|
|

|
|
|
|
|
#8 |
|
Member
Join Date: Mar 2009
Posts: 32
Rep Power: 17  |
>TVD schmes are always used for unsteady problem, and CBC related schemes are used for steady problem.
Is this because TVD schemes are NOT "suitable" for steady computations, and CBC schemes are "suitable" for steady computations? I hate to repeat this, but honestly, I still don't see what is meat by "suitable". Does it mean better accuracy or stability or something else? I'm very interested in your question, and want to understand it. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
Following Hirsch, consider a simple 1D linear advection equation:
 with  . .Then apply, say, the Lax-Wendroff scheme with a time step 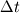 and a grid step and a grid step 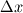 : : with:  What happens in the steady state for this scheme? Just taking  easily give you the answer, which is: easily give you the answer, which is: so your final solution will be dependent on the time step, which is not physical, not at all. This is why this kind of scheme is not suitable for steady state computations. The same reasoning could have be done with the Beam & Warming scheme without any great difference. When considering TVD and CBC almost happens the same thing, to have time accurate solutions you have to include a cfl dependence which, in turn, will remain in the steady state. If this is not the case for the CBC is probably because it is not time accurate, in fact the CBC region in the NVD is different from the projection of the TVD region from the Sweby diagram to the NVD. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| quick scheme in finite difference method | ps | Main CFD Forum | 2 | June 23, 2008 03:02 |
| Unknown Difference Scheme | Jan Christian Dittmer | Main CFD Forum | 8 | August 9, 2005 04:36 |
| High order difference scheme for KIVA3v2??? | LiQiang | Main CFD Forum | 1 | May 9, 2005 14:50 |
| Difference scheme for ALE ?? | LiQiang | Main CFD Forum | 0 | March 26, 2005 22:17 |
| Conservative finite difference scheme? | Linfeng BI | Main CFD Forum | 1 | October 10, 2002 13:17 |