 |
|
|
[Sponsors] | |||||
|
|
|
#41 |
|
Senior Member
|
This work, if i recall correctly, uses explicit filtering by finite volume integration:
http://www.vremanresearch.nl/etc9.pdf still, the details were not described and how conservation was preserved is not exactly clear. I do not exclude that it has to be abandoned in this framework, even if the underlying method is fully conservative like the FVM. Edit: Preservation of the conservation property is one of the reasons Filippo and i worked on its implicit version. |
|
|
|

|
|
|
|
|
#42 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Paolo, the paper of Vreman still do not include a further explicit filtering on the convective flux but, similarily to what I wrote before, consider only the surface integral as the volume filter. However, if I understand, the enlarge the stencil of the integral so that I suppose overlapping volume exists. Conservation should be still ensured by telescopic property .... I feel that including an explicit filtering in the integral-based formulation is not without implication in the formulation. |
||
|
|

|
||
|
|
|
#43 | |
|
Senior Member
|
Quote:
 . But I am not yet convinced that, with that method, conservation is preserved on general grids and with general filter kernels. . But I am not yet convinced that, with that method, conservation is preserved on general grids and with general filter kernels.
|
||
|
|

|
||
|
|
|
#44 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#45 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#46 |
|
Senior Member
|
This thread (topic) is very cumbersome and difficult to find an universal answer. As a matter of fact, at the beginning people used to filter the velocity field separately but then they realized that they needed to filter the convective term. The more I read the least I understand, but Sagaut's book is a very good place to get these answers. Also, professor Denaro has a great experience in this topic.
|
|
|
|

|
|
|
|
|
#47 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
I understand that the issue is not simple and I will try to explain by using the simple Burgers equation:
du/dt + d(u^2/2)/dx = 0 Formally the LES equation is obtained by applying the filter to each term: du_bar/dt + [d(u^2/2)/dx]_bar = 0 This equation is then decomposed in resolved and unresolved fluxes. Now, if you apply a further explicit filter on the convective term (the explicit filter has a greater width than the filter bar), just considering a single time step you see the update of the velocity that has dependence on the form used for the explicit filtering. - Start at t0 with an initial field u_bar(x,0). - compute the resolved convective flux u_bar^2/2 and explicitly filter it with some filter of width greater than the filter _bar. - Compute u_bar(x,0) - time integral of filtered terms. Now, what is the meaning of this field? You see that it depends on the explicit filter, it is no longer the field u_bar(x,dt) that you would obtain using the LES equation without explicit filtering. This fact is also true (and more complex) if you work with the integral instead of the differential formulation. Have you read also this paper of Lund? http://ac.els-cdn.com/S0898122103900...845a8da6fd59d3 |
|
|
|

|
|
|
|
|
#48 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Thanks ... I see that this topic is not simple....I had to study, think and re-study papers. I passed many days working on the equations to understand how to write correctly the LES equation in differential and integral form when are written in continuous form. Further, the difference between implicit and explicit filtering were a troublesome step. Then I had to spend also more time to understand the effect of the discretization on the LES equations. I strongly soggest to use the simple 1D Burgers model to analyse all these aspects. |
||
|
|

|
||
|
|
|
#49 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Alright lets consider the Burgers equation:
 now apply an explicit filter to the equation:  the convective term  has to be decomposed to : has to be decomposed to : One gets then:  So far so good. Now lets descretise the equation in time first:  Lund explains in his paper that all terms on the right hand side contain spectral information upto the cutoff wavenumber of the explicit filter, except for the convective term, since the multiplication of both filtered velocities can generate spectral components above the cutoff wavenumber of the explicit filter (above the bar level). For this reason, he explicitly filters the term  and consequently adjusts the SFS term. One then gets: and consequently adjusts the SFS term. One then gets: Here,  represents the modified SFS term. One can see now that the convective term does not include spectral information above the bar level. Moreover, the second explicit filter used on the whole convective term has the same filter width as the explicit filter used at the begininng. So I don't quiet understand this: represents the modified SFS term. One can see now that the convective term does not include spectral information above the bar level. Moreover, the second explicit filter used on the whole convective term has the same filter width as the explicit filter used at the begininng. So I don't quiet understand this:Quote:
I also don't understand completley the last step you described: by time integral you mean the second term on the RHS of :  ? ?
|
||
|
|

|
||
|
|
|
#50 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
I think that a key to understand the topic, is that the LES equation
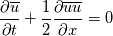 is not then implemented using an explicit filtering but are both the grid and the numerical discretization to act implicitly as filtering. Therefore, the grid introduces the Nyquist filter pi/h and the discretization introduce a smoothing if FD or FV methods are used. The goal of the explicit filtering is to eliminate the numerical error (the smoothing) that the discretization introduce. For doing that, you need that a new Nyquist frequency is introduced by the explicit filtering. Therefore you need a width h'>h so that pi/h>pi/h'. In line of principle, once h' is chosen, you can get a grid independent LES solution for vanishing values of the computational grid h. DO not get into confusion between generation of aliased frequency due to the discretization of the quadratic product and numerical error present also for the linear case. ______________________________ by time integral you mean the second term on the RHS of : 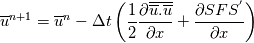 _______________________________ yes |
|
|
|

|
|
|
|
|
#51 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
What you describe here is right. The bars in the equations I worte above are all "explicit filters". The implicit filtering due to discretisation and due to grid cutoff is always there, I just didnt write it in the equations. I am only interested in the explicit filtering. Thats why I said, all bars mentioned above have the same cutoff wavenumber (which is ofcoarse smaller than the grid cutoff wavenumber).
Quote:
 is the filtered velocity at the new time step. Of course its not equal to the velocity I would calculate using just implicit filtering because the non-linear term and in fact all other terms introduce components up to the grid cutoff wavenumber which is greater than the explicit cutoff wavenumber. When using a Fourier-cutoff filter, the calculated is the filtered velocity at the new time step. Of course its not equal to the velocity I would calculate using just implicit filtering because the non-linear term and in fact all other terms introduce components up to the grid cutoff wavenumber which is greater than the explicit cutoff wavenumber. When using a Fourier-cutoff filter, the calculated  would be almost equal to a filtered DNS with the same Fourier-cutoff filter. The only difference between both would be due to the filtering caused by discretisation. would be almost equal to a filtered DNS with the same Fourier-cutoff filter. The only difference between both would be due to the filtering caused by discretisation.Do we both agree on this ? |
||
|
|

|
||
|
|
|
#52 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
[/QUOTE] For me, the computed  is the filtered velocity at the new time step. Of course its not equal to the velocity I would calculate using just implicit filtering because the non-linear term and in fact all other terms introduce components up to the grid cutoff wavenumber which is greater than the explicit cutoff wavenumber. When using a Fourier-cutoff filter, the calculated is the filtered velocity at the new time step. Of course its not equal to the velocity I would calculate using just implicit filtering because the non-linear term and in fact all other terms introduce components up to the grid cutoff wavenumber which is greater than the explicit cutoff wavenumber. When using a Fourier-cutoff filter, the calculated  would be almost equal to a filtered DNS with the same Fourier-cutoff filter. The only difference between both would be due to the filtering caused by discretisation. would be almost equal to a filtered DNS with the same Fourier-cutoff filter. The only difference between both would be due to the filtering caused by discretisation.Do we both agree on this ?[/QUOTE] well, this is a further issue that is debatable... Doing DNS and filtering explicitly the solution is not equivalent to compute the LES solution. First, only for an explicit filtered LES you can apply exactly the same filter on the DNS solution. Second, the filtered LES solution is a direct consequence of the dynamic action of the SGS model. This is not true in the static filtered DNS. However, the comparisons can be performed and, provided you consider the possible difference, they can be useful. |
||
|
|

|
||
|
|
|
#53 |
|
Senior Member
|
Let me first ask you this: why do you think the Lund implementation involves more than one single filter? This is not actually the case... you can see the whole operation just like a spectral dealiasing of the convective term. Moreover, you do not filter the SFS term, but that is typical of eddy viscosity models only. Structural models typically require explicit filtering as well.
Now, if i can, let me give you some perspective. You are treating the whole matter as if it is written in the stone which, if i am allowed to say, is very very far from true. LES and its implementation is made of several pieces which CANNOT be considered separately, unless you just want to have a textbook picture. Most of the past works also explicitly rely on such pictures or, more correctly, do not consider the matter in general, but just from their specific point of view (in terms of numerical implementation). Which is still correct, but does not necessarily apply in general. What happens to the Lund view if, for example, you do not have convection but just diffusion + unsteady term + a linear forcing at some frequencies? Does it means that you can't do explicit filtering on linear equations? |
|
|
|

|
|
|
|
|
#54 | ||
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Quote:
 The tilde corresponds to all implicit filtering effects. The bar corresponds to the use of an explicit filter. Quote:
|
|||
|
|

|
|||
|
|
|
#55 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Quote:
if we don't have the convective term, there is no need for Lund's view in the first place. The absence of the convective term leads to the absence of generating high wavenumber components due to the non-linearity of this term. As a result, all terms on the RHS would consist of wavenumbers up to the curoff wavenumber of the used explicit filter. |
||
|
|

|
||
|
|
|
#56 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
The goal of the explicit filtering in LES is to produce a "bar" velocity cleaned by numerical errors and provide such field to the action of the SGS model. The key is that one wants that the SGS model gets exactly the filtered field you want, without additional numerical effects. In this sense, the LES solution is a consequence of the action of the SGS model. |
|
|
|

|
|
|
|
|
#57 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Again, you are here considering only the aliasing error due to the quadratic product. The numerical error is due to the local truncation error produced by the discretization of the derivative. The action can see by the modified wavenumber analys. The explicit filtering has the aim to eliminate also the local truncation error. |
||
|
|

|
||
|
|
|
#58 | |
|
Senior Member
|
Quote:
1) You assume that your discrete divergence and your discrete gaussian filter commute. 2) You are filtering explicitly, in the sense that every term of uiuj is filtered by a sort of explicit diffusion step. 3) You are trying to discretize the whole thing (which seems exotic). I suspect your problems might come from any of these. Bu you need to give more context for a more serious help: implicit/explicit time integration, compressible/incompressible algorithm, convection scheme, SGS model, etc. For example, in a density based solver, i would just filter explictly the residual on the right hand side (the spatial discretization terms), and that would just work. |
||
|
|

|
||
|
|
|
#59 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#60 | |
|
Member
Join Date: Mar 2012
Posts: 51
Rep Power: 14  |
Quote:
Anyway, the discussion is now diverging from the main problem I was facing, namley filtering the convective term in FVM. I did find a publication where they explicitly filter the convective term in FVM. They just don't mention how they exactly do it (sadly): http://www.measej.ir/files/site1/use...22-5b6c379.pdf They published another paper named: Evaluation of Fourth Order finite volume compact scheme for LES with explicit filtering Unfortunatley, I don't have access to this article. Maybe they described their method in the second paper. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| LES explicit filtering | maka | OpenFOAM Running, Solving & CFD | 4 | December 27, 2012 10:08 |
| LES explicit filtering | Paul | Main CFD Forum | 0 | March 17, 2006 09:03 |
| LES (explicit) filtering | John | Main CFD Forum | 2 | July 29, 2004 19:03 |
| Channel LES and explicit filtering | Luca Liberti | Main CFD Forum | 0 | January 17, 1999 11:07 |