 |
|
|
[Sponsors] | |||||
A problem regarding the calculation of the turbulence index |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Tumul Calm
Join Date: Aug 2023
Location: Europe
Posts: 5
Rep Power: 3  |
hi all, I have a very fundamental, probably borderline stupid question. First a bit background:
I am trying to come up with a consistent methodology that attempts to locate the transition location on blade surfaces in a turbomachine. After spending so much time on many different methods (which were also not applicable to all cases of simulations), I came across a what seems to be a universal yet robust enough formula, i.e. also in the title, turbulence index, from Spalart&Allmaras - "A One-Equation Turbulence Model for Aerodynamic Flows,", 1994. Which is given as below; 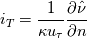 , ,where  is the von karman constant=0.41, is the von karman constant=0.41, 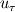 is the friction velocity, is the friction velocity, 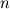 is the wall normal and finally is the wall normal and finally 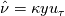 is sort of the modified turbulent viscosity, where is sort of the modified turbulent viscosity, where 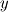 is the wall distance. is the wall distance.My problem is, my normal vector in the software that I am using, is only defined on the solid surface and does not exist for free field. This is a problem since the 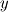 is obviously 0 on the wall so subsequently my all is obviously 0 on the wall so subsequently my all 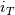 values are also 0. If I'm not wrong values are also 0. If I'm not wrong 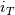 is also not used on the wall but at a small distance. is also not used on the wall but at a small distance.Is there a smart trick that I can use here? For example not using the wall distance=0 on the surface but simply a very small yet constant 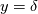 value? Would such a trick violate the validity of this method, just because my wall normal vector does not extend into the free field? value? Would such a trick violate the validity of this method, just because my wall normal vector does not extend into the free field?I know this is a bit futile question as long as one doesn't have the software that I use, but just to gather ideas I wanted to pose this question here. hanks in advance for whatever idea you may suggest me. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
It seems that you need the wall normal derivative of nu_hat.
Depending from where you need it, there are different options. If you just need it at the first cells near a wall, it is pretty easy (you can either approximate it with a one sided difference or directly retrieve the wall normal from the given face where it is available; you could also use the known near wall behavior of nu_hat to compute the derivative analytically). If you need it everywhere, you need to compute the gradient of the wall distance scalar. Depending from which software you are using, it might or not be feasible but, once you get that you just do a scalar product with the nu_hat gradient. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
My first answer was before having a chance to actually read again the S&A paper. Also, I couldn't catch your specification of nu_hat from the email (where latex is not converted).
NO, you aren't supposed to use that formula away from walls (worried about n, think about u_tau now...) AND NO, you aren't supposed to use 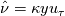 outside the log layer. outside the log layer.So, coming to your question, you can use your formula for  only at walls, where you already have the nu_hat wall normal derivative (i.e., wall diffusion term) or could simply compute it from the cell next to the wall (either one sided at first order or trough cell gradient and wall normal at second order) and you also have u_tau. That's it only at walls, where you already have the nu_hat wall normal derivative (i.e., wall diffusion term) or could simply compute it from the cell next to the wall (either one sided at first order or trough cell gradient and wall normal at second order) and you also have u_tau. That's it
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Tumul Calm
Join Date: Aug 2023
Location: Europe
Posts: 5
Rep Power: 3  |
sbaffini, thank you for answer. glad it ignites a discussion here.
I actually understand that with a self-written code for a finite difference formula (there's no wall normal derivative/wall diffusion term inheritely in the program), I can at worst calculate a simple wall normal derivative and get a first idea as to how  behaves over the blade surface. behaves over the blade surface.However what I cannot wrap my head around is that, we know that 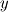 , i.e. wall distance, is , i.e. wall distance, is  on the walls. This already makes on the walls. This already makes 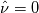 by definition. What am I missing here? Additionally, what about calculating a derivative of a quantity that only exists on wall? My gut tells me there is a subtle way to overcome such a fundamental problem, however my fundamentals knowledge tells me this quantity doesn't make sense. by definition. What am I missing here? Additionally, what about calculating a derivative of a quantity that only exists on wall? My gut tells me there is a subtle way to overcome such a fundamental problem, however my fundamentals knowledge tells me this quantity doesn't make sense.edit: I must say my background on fluid mechanics and cfd is mostly from atmospheric physics. So I was not formally educated on turbomachinery thus lack a bit of familierty on some basic field specifics. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
y=0 on wall means nothing. What you are looking for is the gradient. y=0 on walls for example does not mean the wall normal velocity gradient, pressure gradient or wall normal temperature gradient is zero (unless it is the BC). This isn't specific to one industry, it's a fundamental misconception.
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
Quote:
Imagine a function f like: f = an + b then you have df/dn = a. As you can probably better see now, b doesn't affect df/dn. Now, your nu_hat is indeed 0 at walls by definition, but certainly not its derivative (unless it turns out so from the computation). P.S. For equilibrium boundary layers nu_hat is meant to be linear from the wall up to the end of the log-layer (my bad, in my previous post I wrongly worded this concept, and it seemed that it holded ONLY in the log-layer, which is not). Still, this is not valid in general so, again, don't rely on this in general. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Tumul Calm
Join Date: Aug 2023
Location: Europe
Posts: 5
Rep Power: 3  |
Hi again, thank you once more for comments. I think I have to explain myself more in detail. Essentially the problem of evaluating this term at the wall apeears when we look at the expansion of the derivative:
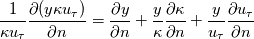 In above equation 2nd term is 0, regardless of where you evaluate it since  is a constant. 3rd term is not 0 in the free field, but 0 at the wall, since is a constant. 3rd term is not 0 in the free field, but 0 at the wall, since 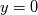 at the wall. Then all we are left is at the wall. Then all we are left is 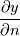 , which in no way measures any turbulent condition from a given system. , which in no way measures any turbulent condition from a given system.Am I making a mistake here with the expansion? |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
I'm not sure where you are even going with this expansion.
You have committed the grave sin of dividing by 0. 0/0 is not 1. Hence, you are in fact, not left with only dy/dn Additionaly, y is n and you have arrived dn/dn is ???? which it should be the identity relation. And of course, that clearly tells you nothing. Put another way, if I say df/dy = df/dy and I put in y=0, that still doesn't tell me anything because I never knew what was df/dy to begin with. |
|
|
|

|
|
|
|
|
#10 | |
|
New Member
Tumul Calm
Join Date: Aug 2023
Location: Europe
Posts: 5
Rep Power: 3  |
Quote:
excuse me but you are not being polite, why are you spending time with these words instead of showing what you see wrong? I highly suspect that you are fighting with an imaginary person in your head. Coming back to the discussion, where is the division by 0?? y is not n btw, y is the closest distance to the wall, where n is normal to the blade surface. towards hub and shroud surfaces there is significant difference between the two. from this point on I will only reply to people who are taking my point seriously and not lose time try to repeat the same things over and over again. |
||
|
|

|
||
|
|
|
#11 | |
|
Senior Member
|
Quote:
In addition to this, note that u_tau is only defined at walls. It only exists there because its definition involves a derivative taken at the wall. You could, kind of arbitrarily, associate an u_tau to a fluid point away from walls by locating the nearest point on a wall and its associated u_tau, but that's not how u_tau should be used in general (also, equilibrium flows are, again, special). So, again, forget your expression for u_tau and just compute the derivative as in the original expression which, let me further clarify it, just involves two wall derivatives and k, so it is only valid at walls and/or their adjacent cells. |
||
|
|

|
||
|
|
|
#12 | |
|
New Member
Tumul Calm
Join Date: Aug 2023
Location: Europe
Posts: 5
Rep Power: 3  |
Quote:
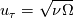 , for , for 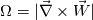 , which is suggested to be used by Spalart&Allmaras('92). It definitely shows me interesting results, however they are not perfectly correct. , which is suggested to be used by Spalart&Allmaras('92). It definitely shows me interesting results, however they are not perfectly correct.Not to prolonge the discussion unnecessarily but for anyone who might see this and want to know what I did, I simply took the derivative as: 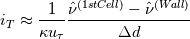 , ,where  is the distance between the blade wall and the first cell. A typical is the distance between the blade wall and the first cell. A typical 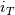 distribution should show a sharp change from 0 to 1, right around the location of transition from laminar to turbulence. Values I get seem to find very well the approximate transition location however there's no sharp change from 0 to 1 whatsoever. It hovers from blade tip until the transition between 0.7-0.9 and then after the transition goes above 1. These results could be very well specific to my simulated case (for example, I am not sure how much this index is valid for internal flows, almost all examples I found of its usage was applied on external flows...), however for my initial attempt it seems to be not entirely but somewhat wrong. distribution should show a sharp change from 0 to 1, right around the location of transition from laminar to turbulence. Values I get seem to find very well the approximate transition location however there's no sharp change from 0 to 1 whatsoever. It hovers from blade tip until the transition between 0.7-0.9 and then after the transition goes above 1. These results could be very well specific to my simulated case (for example, I am not sure how much this index is valid for internal flows, almost all examples I found of its usage was applied on external flows...), however for my initial attempt it seems to be not entirely but somewhat wrong.
Last edited by tumultous_calmness; October 15, 2024 at 08:49. |
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
|
Quote:
1) u_tau is not random, or sort of, it has to be computed in the exact same way it enters the computation (tau_wall = rho u_tau^2) 2) tau_wall involves the wall normal derivative of the wall parallel velocity at the center of the cell face on the wall, not some quantity evaluated at the near wall cell center 3) the nu_hat wall normal derivative must be taken in the same way of the one involved in tau_wall, which implies taking care of the correct wall normal and distance for non regular grids Now, there might be reasons for which you can't do all of this, but I would consider them mandatory before any futher inquire on the method and/or implementation |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Problem in Torque calculation | Achilleas | CFX | 21 | July 25, 2018 10:14 |
| Turbulence postprocessing | Mohsin | FLUENT | 2 | October 3, 2016 15:18 |
| Problem in Torque calculation | Achilleas | ANSYS | 0 | October 1, 2015 09:56 |
| divergence problem with turbulence | tH3f0rC3 | OpenFOAM | 4 | April 6, 2011 11:14 |
| Starwatch problem and turbulence length unit | Jiaying Xu | Siemens | 0 | August 18, 2001 11:57 |