 |
|
|
[Sponsors] | |||||
Asking help on derivation of ALE differential form of momentum conservation equation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
pengfeiguo
Join Date: Nov 2017
Posts: 10
Rep Power: 9  |
I want to find the differential equation form of momentum conservation equation that holds at any point
within an arbitrary moving and deforming grid, i.e., the momentum differential equation in ALE description. After reading the wonderful book "fluid mechanics" sixth edition by PIJUSH K. KUNDU et. al, i.e., equation 4.17, if I understan right, the ALE form of Reynolds transport is 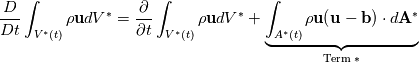 Let handle the volume intergral in the above equation as 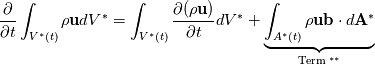 You see that when I moved the differentiation into the integral, a surface integral term (Term**) containing the boundary velocity appeared. This term would cancel out the term containing the surface velocity (  ) in the Reynolds transport equation, ) in the Reynolds transport equation, ultimately leading to the absence of surface velocity in the transport equation. I believe this is an incorrect result. Can you give me some suggestions on where I am doing wrong? Thanks! Sincerely, Guo Pengfei Last edited by pfguo; April 30, 2024 at 05:51. Reason: edit for more clear question |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Jul 2009
Posts: 358
Rep Power: 19  |
Try using Gauss' theorem to convert the area integrals to volume integrals. Then you have to make the argument that if the integral equals to zero then under sufficient conditions for continuity of the integrand that the integrand must equal zero over the domain. Since these conditions fail in the presence of discontinuities most people use the integral form, or figure out the singular limit conditions to apply to the jumps where the differential form is invalid.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Jul 2009
Posts: 358
Rep Power: 19  |
You will also need to move the temporal derivative inside the volume integral, even in the case of deforming boundaries. There is a mathematical theorem to handle that also - I'll leave that as an exercise for the reader.
|
|
|
|

|
|
|
|
|
#4 | |
|
New Member
pengfeiguo
Join Date: Nov 2017
Posts: 10
Rep Power: 9  |
Quote:
Actually, I got stuck even before applying the divergence theorem to the surface integral term. I got stuck on the term involving the derivative of the volume integral with respect to time. When I moved the differentiation inside the integral, a surface integral term (Term**) containing the boundary velocity appeared. This term would cancel out the term containing the surface velocity (  ) in the Reynolds transport equation, ) in the Reynolds transport equation, ultimately leading to the absence of surface velocity in the transport equation. I believe this is an incorrect result. By the way, for better readability, I spent some time replacing the original image with LaTeX formulas 
|
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Join Date: Jul 2009
Posts: 358
Rep Power: 19  |
Are you sure you aren't applying Liebniz's theorem twice? Consider mass conservation for a fluid element - mass conservation in a Lagrangian sense is simply the time derivative of the integral of density over the volume is zero. Then you can apply Liebniz's theorem to get the equation where the temporal derivative is inside the integral and the relative velocity appears in the area integral. Then apply divergence to that. It seems like you are double-counting the surface velocity.
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Just follow the idea of the derivation of the Reynolds transport theorem.
You can read a rigorous description in the textbook of Chorin & Marsden. |
|
|
|

|
|
|
|
|
#7 | |
|
New Member
pengfeiguo
Join Date: Nov 2017
Posts: 10
Rep Power: 9  |
Quote:
|
||
|
|

|
||
|
|
|
#8 |
|
New Member
pengfeiguo
Join Date: Nov 2017
Posts: 10
Rep Power: 9  |
Thank you for recommending the book. I've been reading it for a while, but I'm still unclear about where my problem lies. Nevertheless, I sincerely appreciate your attention.
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
||
|
|

|
|
|
|
|
#10 |
|
New Member
shristi
Join Date: Jun 2023
Posts: 26
Rep Power: 3  |
Hello,
I am working on the FSI problem for vortex-induced vibration. The ALE approach has been used to solve coupling motion for fluid and solid. The fluid equation is discretized based on FVM, and the structure equation is the newmark method used, and that is FEM. However, I am not sure about how the mesh motion equation, which is a Laplacian equation, is solved to update mesh motion velocity. and also, don't you know if this method is used for it FVM or FEM? Please help me to clear this up and also suggest some books that can give a good understanding of the ALE approach computationally. I am using OpenFOAM for my computations. Thank you |
|
|
|

|
|
|
|
|
#11 |
|
New Member
pengfeiguo
Join Date: Nov 2017
Posts: 10
Rep Power: 9  |
Thank you for your suggestion.
I have been reading the content you mentioned in the book you recommended these past few days. Basically, I can understand the proofs in the book, but it doesn't relate directly to the question I asked. I kindly request you to read my question again. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Adding a term in the diagonal of the matrix form of the momentum equation | Agavi | OpenFOAM Programming & Development | 1 | August 3, 2020 14:12 |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 06:21 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 07:27 |
| Question on the discretization of momentum equation in icoFoam | MPJ | OpenFOAM | 3 | October 4, 2011 10:44 |
| Constant velocity of the material | Sas | CFX | 15 | July 13, 2010 09:56 |