 |
|
|
[Sponsors] | |||||
Solving Navier-Stokes Numerically (Discretization) |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Kokogu
Join Date: Mar 2024
Posts: 3
Rep Power: 2  |
Unsteady, incompressible, laminar and fully developed flow inside a circular pipe can be expressed by following the 1D parabolic PDE form of the Navier-Stokes equation where u(r,t) is to be calculated.
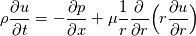 Boundary conditions for the problem are symmetry at the centre and no-slip on the walls. Initially, the fluid is at rest. 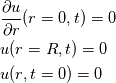
Last edited by kokogu; March 19, 2024 at 15:39. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,762
Rep Power: 66    |
https://en.wikipedia.org/wiki/Crank%...icolson_method
see also the table on forward euler and backward euler for a very obvious hint on how to do those cases as well |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Kokogu
Join Date: Mar 2024
Posts: 3
Rep Power: 2  |
Quote:
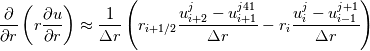 Maybe like this? But I could not grasp why are we doing smth like this. Also I am gonna solve this with MATLAB Last edited by kokogu; March 19, 2024 at 15:40. |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
This is just the formula obtained by the successive discretization from the outer to inner operator d/dx using a centred second order discretization on the step dr. This is done to avoid a larger stencil having the issue of the checkerboard modes. |
||
|
|

|
||
|
|
|
#5 |
|
New Member
Kokogu
Join Date: Mar 2024
Posts: 3
Rep Power: 2  |
Could you help me discretize this? For FTCS, BTCS, and Crank-Nicolson Method.
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,762
Rep Power: 66    |
Quote:
Furthermore, the general N-S and other important PDE's are non-linear. In this example you start with the parabolised navier-stokes which is linear to begin with. But discretizing a non-linear PDE also results in the same algebraic equations (for FTCS) and linear system (for BTCS and CN). The reason you are being assigned parabolised navier-stokes, is the discretization is simple and it facilitates learning how to discretize PDE's. Clearly if students struggle with discretizing the parabolised navier-stokes equations, then the full navier-stokes is even more daunting and then students baby-rage and quit prematurely. |
||
|
|

|
||
 |
| Tags |
| btcs, discretisation, ftcs, navier stokes equation, navier-stokes solver |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Segmentation fault when using reactingFOAM for Fluids | Tommy Floessner | OpenFOAM Running, Solving & CFD | 4 | April 22, 2018 13:30 |
| HeatSource BC to the whole region in chtMultiRegionHeater | xsa | OpenFOAM Running, Solving & CFD | 3 | November 7, 2016 06:07 |
| Floating point exception error | lpz_michele | OpenFOAM Running, Solving & CFD | 53 | October 19, 2015 03:50 |
| Cannot run the code properly: very large time step continuity error | crst15 | OpenFOAM Running, Solving & CFD | 9 | December 14, 2014 19:17 |
| calculation stops after few time steps | sivakumar | OpenFOAM Running, Solving & CFD | 7 | March 17, 2013 07:37 |