 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I am examining a 1D rod using mass co-ordinates under the effect of gravity. I have the rods on their end so that gravity will assist it. The equations are specific volume
 and u, the velocity. The mass co-ordinate is given by: and u, the velocity. The mass co-ordinate is given by: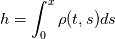 The equations are then: 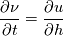 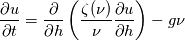 I'm unsure about what should happen. For the application, the length should monotonically decrease. Do you have any idea what's going on? Code:
%this code solves the following system of equations:
%v_t=u_h
%u_t=(zeta/v*u_h)_h
%dX/dt=u
%h is defined by h_x=1/v, and X is the new position of the interfacial
%points
%The boundary conditions for u is u(t,0)=0, u_h(t,1)=-v(t,1)
%The BC's for v, can be derived from ones on u.
%here u is the velocity, and v is the specific volume defined as 1/rho, where rho is the density
%The system is in conservative form, and the finite volume method is the best method for these types of equations
clear;clc;
S=struct;
%---define physical constants
N=200; %This is the number of cells in the simulation
S.N=N;
S.alpha=0.2;
c_p=1; %heat capacity.
rho_half(1:N)=0.6; %This is the initial density
eta_0=0.005;
S.eta=eta_0;
M=300; %This is the number of points in the time domain.
%---Set up geometry
x=linspace(0,1,N+1); %Initial spacing of the cell interfaces and ends.
dx=x(2); %initial lengths of cells
t=linspace(0,300,M); % This is the time of integration
L=zeros(M,1); %The length of the of the piece
L(1)=1; %Initial length
dt=t(2); %time increment
S.dt=dt;
mu=dt/dx^2;
%---Set up of variables
nu=zeros(M,N); %The specific volume =1/density
u=zeros(M,N); %The speed of the material
X=zeros(M,N+1); %The position of cell interfaces
X(1,:)=x;
%---The solution of the system will be done via Newton-Raphson. The two
%variables v and u will be put into one vector y=[v u]'
y_old=zeros(1,2*N); %This is the initial vector used.
nu(1,:)=1./rho_half; %Initial specific volume
y_old(1:N)=nu(1,:);
%v(1,:)=y_old(N+1:2*N);
theta=0.5-1/(12*mu); %This will meximise the timestep.
rho_0=zeros(1,N+1); %This sets up the calculation for h to begin with.
%This interpolates the density from the cell centres to cell boundaries.
rho_0(2:N)=0.5*(rho_half(1,N-1)+rho_half(2:N));
rho_0(1)=1.5*rho_half(1)-0.5*rho_half(2);
rho_0(N+1)=1.5*rho_half(N)-0.5*rho_half(N-1);
h=cumtrapz(x,rho_0); %calculates h, which is used throughout the timesteps.
nu_m(1:N)=1; %This is the matal powder density, the maximum possible density.
S.nu_m=nu_m;
dh=diff(h); %This is used to approximate the derivative
S.dh=dh;
tol=1e-5; %Tolerance on the Newton-Raphson method.
dx=diff(x);
for i=2:M
y_init=1.001*y_old; %This is an initial guess for the new solution forbased upon the previous timestep solution
y = Newton(tol,y_old,y_init,theta,S); %call the Newton Raphson routine
nu(i,:)=y(1:N); %First N entries are the specific volume
u(i,:)=y(N+1:2*N); %the second entries are the velocities
%Compute the new grid
dX=dh.*nu(i,:); %The mass in each cell in constant, use density*length=mass to compute the new length of the cell
X(i,2:N+1)=cumsum(dX); %x(2:N+1)-(dx-dX); %Update the Eulerian co-ordinates.
L(i)=X(i,N+1); %The length of the rod is the last entry
y_old=y; %Set the new solution as the old one.
end
plot(t,L)
r_half=1./nu(end,:);
X_half=0.5*(X(end,1:N)+X(end,2:N+1));
r=interp1(X_half,r_half,X(end,:));
v=interp1(X_half,u(end,:),X(end,:));
figure;
plot(X(end,:),r);
xlabel('X(t)')
ylabel('Density');
figure;
plot(X(end,:),v);
xlabel('X(t)')
ylabel('Velocity');
% function y=mass_flux(nu,u)
% global N
% global dh
% y=zeros(1,N+1);
% y(2:N)=0.5*(u(2:N)+u(1,N-1));
% y(N+1)=u(N)-0.25*dh(N)*(3*nu(N)-nu(N-1));
% end
function y=flux(u,nu,S)
%This computes the fluxes required for the finite volume method
N=S.N;
dh=S.dh;
nu_0=S.nu_m;
k=0.01;
a=0.01;
nu_end=1.5*nu(N)-0.5*nu(N-1);
nu_0_end=1.5*nu_0(N)-0.5*nu_0(N-1);
y=zeros(2,N+1); %This vector will store the fluxes for the mass and momentum
y(1,2:N)=0.5*(u(2:N)+u(1,N-1)); %Fluxes for the mass
y(1,N+1)=u(N)-(nu_end*k/zeta(nu_end,nu_0_end,S))*dh(N)/2;
nu_face=0.5*(nu(1:N-1)+nu(2:N)); %This is specific volume on the cell interface
y(2,2:N)=P_L(a,nu_face,nu_0(2:N))+(4*zeta(nu_face,nu_0(2:N),S)./nu_face).*((u(2:N)-u(1:N-1))./(dh(2:N)+dh(1:N-1))); %The flux for the momentum equation
%nu_L=1.5*nu(1)-0.5*nu(1); %the specific volume at the end
nu_L=nu(1)+dh(1)*(nu(2)-nu(1))/(dh(1)+dh(2)); %The matal powder specific density
%nu_0_L=1.5*nu_0(1)-0.5*nu_0(1);
nu_0_L=nu_0(1)+dh(1)*(nu_0(2)-nu_0(1))/(dh(1)+dh(2));
y(2,1)=P_L(a,nu_L,nu_0_L)+(zeta(nu_L,nu_0_L,S)/nu_L)*(2*(u(2)-u(1))/(dh(1)+dh(2))); %the fluxes at the end
y(2,N+1)=0;
end
function y=P_L(a,nu,nu_0) %This is the laplace pressure
x=1-nu_0./nu; %This is the porosity for an imcompressible metal powder
y=a*(1-x).^2;
end
function y=zeta(z,nu_0,S)
eta_0=S.eta;
x=1-nu_0./z;
y = 2*(1-x).^3*eta_0./(3*x);
end
function [J] = jacobian(y_old,y,theta,S)
% Computes the Jacobian matrix of the function f(x)
% f: function handle that returns a vector of function values
% x: column vector of independent variables
% Number of function values and independent variables
n = length(y); % number of independent variables
% Initialize Jacobian matrix
eps=1e-5; % could be made better
J = zeros(n,n);
T=zeros(1,n);
for i=1:n
T(i)=1;
fPlus = sintering_RHS(y_old,y+eps*T,theta,S);
fMinus = sintering_RHS(y_old,y-eps*T,theta,S);
J(:,i) = (fPlus-fMinus)/(2*eps);
T(i)=0;
end
end
function f=sintering_RHS(y_0,y,theta,S)
%the vector f has the stencil for each cell for both the mass and momentum
nu_m=S.nu_m;
dt=S.dt;
N=floor(length(y)/2);
f=zeros(1,2*N);
flux_1=flux(y(N+1:2*N),y(1:N),S); %This is flux at timestep i
flux_0=flux(y_0(N+1:2*N),y_0(1:N),S); %this is the flux at timestep i-1
f_mass=flux_1(1,:);
f_mom=flux_1(2,:);
f_mass_0=flux_0(1,:);
f_mom_0=flux_0(2,:);
f(1:N)=y(1:N)-y_0(1:N)-dt*theta*(f_mass(2:N+1)-f_mass(1:N))-(1-theta)*dt*(f_mass_0(2:N+1)-f_mass(1:N)); %These are the stencils coming from the system of equations
f(N+1:2*N)=y(N+1:2*N)-y_0(N+1:2*N)-dt*theta*(f_mom(2:N+1)-f_mom(1:N)-S.alpha*y(1:N))-(1-theta)*dt*(f_mom_0(2:N+1)-f_mom_0(1:N)+S.alpha*y_0(1:N));
f(1)=y(1)-y(2);
end
function [y] = Newton(tol,y_old,y0,theta,S)
iter = 0;
maxiter = 10;
error=10;
J0 = jacobian(y_old,y0,theta,S); %Computes Jacobian
J_inv=inv(J0);
%[L,U] = lu(J0);
while (error > tol) && (iter < maxiter)
%J0 = jacobian(y_old,y0,theta); %Computes Jacobian
f_old=sintering_RHS(y_old,y0,theta,S); %Computes the old f
delta_y = -J_inv*f_old'; %Computes the differencebetween old and new guesses
y = y0 + delta_y'; %the new guess
error=norm(sintering_RHS(y0,y,theta,S)); %computes the error, the error should be very small
y0 = y;
iter = iter + 1; %Updates the iteration
% fprintf('Iteration %i, norm = %.2f\n', iter, error)
end
end
|
|
|
|

|
|
 |
| Tags |
| cfd |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Conflicting length scale definition | jonasa97 | CFX | 12 | February 4, 2023 15:38 |
| Odd behaviour in circuitBoardCooling | sturgeon | OpenFOAM Running, Solving & CFD | 3 | April 26, 2018 09:22 |
| Odd residual behaviour for Two Layer K Epsilon | dvcauwe | Main CFD Forum | 1 | March 7, 2012 06:47 |
| extrudeMesh - odd behaviour | grjmell | OpenFOAM | 0 | September 20, 2011 09:41 |
| Odd behaviour in wigleyHull in OF 2.0 | msbealo | OpenFOAM Running, Solving & CFD | 0 | July 16, 2011 06:53 |