 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Suppose I have a rectangular cell with vertices at
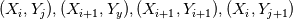 , If we label the sides, in the obvious way as , If we label the sides, in the obvious way as 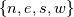 . The finite volume method yields the derivatives evaluated at the cell sides, and . The finite volume method yields the derivatives evaluated at the cell sides, and I know how to approximate: 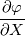 on the east, and west faces using Taylor series is a simple way. However, I am confused about how to do it on the north, and south sides. I thought about taking averages around the north(or south) edge. 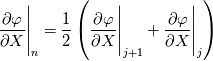
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
That depends on the choice you did for the colocation of phi. Is it at the FV center X(i+1/2),Y(j+1/2) or is cell-vertex ?
It seems a cell-center colocation, thus you need of an interpolation. But why do you need a tangential derivative on the faces? In a FV scheme it never enters into the update. |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The normal component of the tensor has tangential derivative ? Then yes, use a linear interpolation.
|
|
|
|

|
|
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Matlab code for Finite Volume Method in 2D | coagmento | Main CFD Forum | 5 | October 7, 2022 14:47 |
| The fundamental difference between Finite Difference and Finite Volume Methods | vikramaditya91 | Main CFD Forum | 3 | January 14, 2016 05:13 |
| Problem with SIMPLEC-like finite volume channel flow boundary conditions | ghobold | Main CFD Forum | 3 | June 15, 2015 12:14 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| influence of convex or concave control volume in finite volume discretization | openfoammaofnepo | Main CFD Forum | 1 | March 24, 2014 03:13 |