 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I am thinking about the finite volume in 2D. Suppose I have a rectangle, A with vertices:
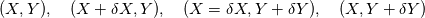 One of the equations I have to solve is: 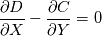 So the usual way is to integrate around the rectangle I mentioned and I get the following calculation: 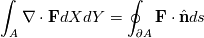 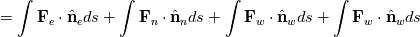 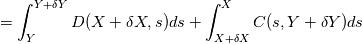 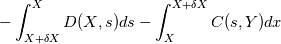 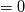 So far this makes sense to me as to what I'm doing. I can then use the midpoint rule to approximate the integral. Is what I'm doing correct? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Before the last line you need to declare/decide/invoke a discretization scheme for each face flux Fe,Fw,Fn,Fs. The surface integrals will become a summation naturally
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
The usual way is to consider the cell centered values the primitive variables. So by writing D(X+dx) etc you are invoking an discretization scheme since face fluxes are determined by the discretization scheme.
Well fine, then write down what exactly is D(X+dx) The integral is no issue, it's just face flux that you sum over cells. No fancy midpoint integration rules needed to approximate the integral. The approximation is frontloaded on the discretization scheme. |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
I could choose any points for my rectangle. |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Some observations:
1) define e vector f having cartesian components (fx=D, fy=-C). 2) the volume integral of the divergence is equal to the surface integral of the normal component of f: Int[Y; Y+dY] [fx|x+dx -fx|x ]dy +Int[X; X+dX] [fy|y+dy -fx|y ]dx=0 This equation is exact. 3) Now, the task of the discretization requires to define how do you colocate the variable on a computational grid. There are different choices, what do you want to use? I suppose your variable is at (X+dX/2, Y+dY/2), right? |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#9 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Yeah the discretization is not unique. You must choose something. In this case the choice is quite intuitive. But from your previous posts, I get that you are not following the logical steps and so that's why I'm asking you to pick a discretization scheme and be aware that you are picking one.
What I don't want to hear, is after blindly applying a discretization scheme without realizing it, you claim that the subsequent equations are "exact." You cannot simple evaluate D(X+dx,Y+dy) wherever you like for arbitrary dx and dy. Do a taylor series about the cell centered values... Unless your radius of convergence is infinite, your taylor series is guaranteed to converge only at dx=0,dy=0. See's taylor's theorem. At any other dx, dy, there is a potential error and therefore your face fluxes are never exact. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I've not thought about discretisation yet. I was going to just get this far and then think about it as the next step. Second order seems like the thing to do though. The goal is to get something working and then think about how to make it more accurate/faster.
|
|
|
|

|
|
|
|
|
#11 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
You've chosen D(X+dx) to evaluate your face fluxes (which is a corner node, not a face center nor a cell center). That is a discretization scheme. And you something think this is mathematically exact... exactly as I feared. Your title suggests you are doing FVM. So I'm expecting FVM and discete, non-continuous math.
|
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I think that the meaning of the original post is only to write the exact surface integral of the normal component of the flux, that is
Int[S] n.f dS on a generic 2D Cartesian volume. And yes, that results in an exact equation. Discretization starts when we discuss the discrete counterpart of the integral and the discrete counterpart of the flux reconstruction from the primitive variables. |
|
|
|

|
|
|
|
|
#15 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Quote:
These are not the integral forms of the governing equations, please don't mix them up. What you have done is taken the PDE, integrated them over the control volume, and applied the Gauss Divergence theorem. |
||
|
|

|
||
|
|
|
#16 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
However, we can assume valid in this discussion both way. The key is that the equation discussed in this post is not derived as conservation form. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Looking at the original post again I see that Divergence theorem is not being applied but rather it is Green's theorem. So this approach would not result in the typical FVM
|
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
no problem, it is practically the same https://en.wikipedia.org/wiki/Divergence_theorem The only note is the in the FVM you divide for the measure of the volume, this way for |V|->0 you get the differential form. |
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Ok I see now the equivalency for the special case of 2D.
|
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I think I am pretty comfortable with what I've done. Constructing the fluxes for the main equations will be messy, but not anything that I can't overcome.
|
|
|
|

|
|
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| finite volume method and finite difference method | harishkamat100 | FLUENT | 3 | December 22, 2020 00:52 |
| Finite element method ANSYS CFX | tomd97 | CFX | 2 | April 4, 2018 05:10 |
| Mesh; wall function for element based finite volume method | sheaker | CFX | 2 | January 25, 2018 18:36 |
| ALE in finite volume method | littlelz | Main CFD Forum | 5 | June 21, 2003 13:50 |
| finite volume method for CFD analysis of 2D blunt body | Aditya Vaze | Main CFD Forum | 1 | January 19, 2000 14:55 |