 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Suppose I have the system:
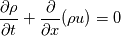 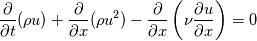 written in Eulerian co-ordinates, and I wish to write it in Lagrangian co-ordinates. I would normally use the Piola transformation to obtain the equations of motion. However, when I have a secopnd order equation like the one I stated, would I have to use the chain rule to convert the first order equations into Lagrangian co-ordinates to complete the transformation? 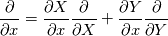 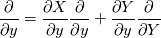 Is there a compact notation for this? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
it's the Jacobian. What am I missing?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Matrix notation d = J.d' you can see the trasformation in the book of Chorin &Marsden in the description of the Reynolds transport theorem. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I managed to work it out in the end.
|
|
|
|

|
|
 |
| Tags |
| piola transformation, viscosity |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Eulerian Multiphase Model vs Lagrangian Particle Tracking | ajjadhav | CFX | 14 | December 7, 2020 17:22 |
| converse lagrangian field to eulerian | Jan_B | OpenFOAM Programming & Development | 0 | August 13, 2015 14:11 |
| lagrangian and eulerian representaions | kakollu | Main CFD Forum | 14 | February 12, 2010 12:35 |
| Arbitrary Lagrangian Eulerian Methods | Soheyl | Main CFD Forum | 1 | June 12, 2006 04:42 |
| Comparison between Eulerian and Lagrangian Models | Ricardo Damian | CFX | 0 | September 3, 2001 20:13 |