 |
|
|
[Sponsors] | |||||
|
|
|
#121 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I just had a further check, you could linearize the equation for u and solving for u(i+1) with a Thomas algorithm and then solve the mass equation where u(i+1) is known. |
|
|
|

|
|
|
|
|
#122 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#123 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#124 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
I will add that I tried to do this using ode15 and that crashed as well which was annoying. |
||
|
|

|
||
|
|
|
#125 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The linearization would produce a simple linear algebric system, no Jacobian is required! In the matrix entries you have all functions that are known at time i. The matrix is tridiagonal and you solve with Thomas. |
||
|
|

|
||
|
|
|
#126 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
This is going to be a major change to the code. I would need to predefine the matrices wouldn't I? I can't simply define them numerically that I can using NR. |
||
|
|

|
||
|
|
|
#127 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
It's a waste of computational resource and time. You have a tridiagonal matrix, memorized in only three vectors a,b,c. Stop. The Thomas algorithm is a two lines code. There is no sense in invoking the use of NR. |
||
|
|

|
||
|
|
|
#128 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
How would I go about this? Is there a quick way to obtain the matrix?
|
|
|
|

|
|
|
|
|
#129 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The operator that one gets from the CN scheme applied on the diffusive term I-(dt/Re)d^2/dx^2 can be inverted, for dt/Re, small as [I-(dt/Re)d^2/dx^2]^-1=I+(dt/Re)d^2/dx^2 + ... that would make explicit the solution. |
||
|
|

|
||
|
|
|
#130 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
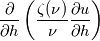 Are you suggesting that I don't use the FVM anymore with this? |
||
|
|

|
||
|
|
|
#131 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Thomas algorithm is just the solver for the linear system as opposed to brute forcing it with gaussian elimination, SORm CLU, or using / in matlab. The linear system is the same whether you solve it with thomas or gaussian elimination or / or your wonky newton raphson. Ax=b doesn't suddenly not become Ax=b just because you change the solver.
If you are actually using / in matlab then you are done. But then you shouldn't also be doing Newton Raphson. Clearly you haven't built the proper linear system that should arise when you do FVM + implicit CN. Trust me in the old days of matlab where it didn't support matrix division I also used to spam fsolve to solve linear systems because I was too lazy to code up my own linear solvers. It is a relic of the past. Let it be buried there. |
|
|
|

|
|
|
|
|
#132 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I am focusing on the LHS of the equation, that is how you get the entries of the matrix. If you look at the LHS, you see something like (I-alpha*A).u=q for small alpha value, an approximation would be u=(I+alpha*A+...).q without solving the system you can get an expression for the solution. But forget this method, just solve for u using the Thomas algorithm or any other solver you want. |
||
|
|

|
||
|
|
|
#133 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#134 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#135 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I seem to be having an error. To compute the new position of the interfacial points I solve:
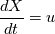 But I get silly answers for the new values. Do I need to remap at each timestep? The remap involves the Jacobian, so how do I compute the new Jacobian? I'm now assuming that once I have computed the new Jacobian, I then solve: 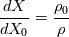 to get the new proper co-ordinates? |
|
|
|

|
|
|
|
|
#136 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I suppose your domain is shrinking, the shift of the interfacial point requires a remapping when the last cell reaches a negative volume. That could be easily, just modify only the cell where the interfacial point lies and let the others. |
|
|
|

|
|
|
|
|
#137 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
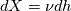 If dx is the original length, I can compute the difference as dx-dX>0, and I simply take that away from the original length. |
||
|
|

|
||
|
|
|
#138 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I've been running my code and I have a rather odd phenomenon in that the density. I have computed the fluxes at all interface points, including the boundary. The density at x=0 should remain the same for small times but it changes. There is no a priori no-flux condition at x=0, but it's not physical, and I don't understand what is going on exactly.
I have included a screen shot. |
|
|
|

|
|
|
|
|
#139 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Let me resume your problem to be sure. 1) At x=0 you have the condition u=0 but you do not fix a value for density? 2) At x=0 you have the face of the first finite volume, that is the first equations is resolved at x=dx/2, right? 3) Thus, the convective mass flux is zero at x=0 but mass will slowly increase because you have a negative velocity profile, so that mass enter from the right face at x=dx. 4) The lagrangian scheme you are using involves a diffusive flux at x=0? |
||
|
|

|
||
|
|
|
#140 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
2) Essentially, the first cell is at dh/2. 3) There is a diffusion equation for the velocity. The negative velocity is diffused in at h=1. 4) Yes. |
||
|
|

|
||
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| multiphaseEulerFoam FOAM FATAL IO ERROR | qutadah.r | OpenFOAM Running, Solving & CFD | 11 | December 10, 2021 21:18 |
| SU2 7.0.7 Built on CentOS 7, parallel computation pyscript mpi exit error? | EternalSeekerX | SU2 | 3 | October 9, 2020 19:28 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| Gradient evaluation in Finite Volume Methods | yidongxia | Main CFD Forum | 7 | August 6, 2012 11:23 |
| Unstructured grid finite volume methods | Marcus | Main CFD Forum | 3 | December 5, 2000 01:25 |